Yoav Y. Schechner: Research
Rotating Beams
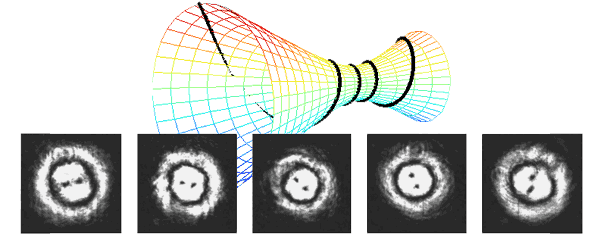
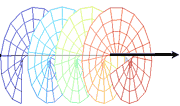
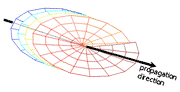
We have performed a line of studies dealing with rotation effects in waves, e.g., light. Here we do not refer to circular polarization (vector waves), but to scalar properties: intensity and phase. The work deals with propagation that resembles a helical trajectory in free space. This is impossible for light rays, since rays travel in straight lines. However, considering the wave nature (not ray) of light, propagation is not in straight lines but exhibits diffraction. Hence, diffraction can create rotating patterns. This work has both theoretical implications, and a practical benefit in the form of a depth (3D) sensing method, as detailed below.
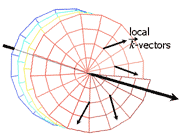
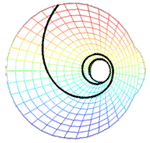
The first waves we studied have rotating spatial distribution of phase, while their intensity pattern may not rotate (wave dislocations). We parameterized such waves, for a general case where the phase rotation and intensity distribution (around the propagation axis) are anisotropic. One parameterization is morphological. The other is as a superposition of isotropic waves, particularly the Gauss-Laguerre complete orthogonal set of functions. It encapsulates information about orbital angular momentum of the wave.
Then, the isotropic basis (Gauss-Laguerre) is used for deriving the general set of waves whose intensity distributions rotate around and along the propagation axis (rotating beams). We recently used such waves for measuring depth. The accuracy of classical depth-from-defocus methods has been limited by the depth of field of the imaging system. However, we show that if the system's point-spread function (PSF) is a rotating beam, then depth discrimination is significantly improved, relative to estimation based on standard defocus PSFs. This enhanced capability is quantified using both an information theoretic criterion and MSE. Experimentally, we demonstrated such rotating beams using computer-generated holograms.
Back to basic research, we extended our study in wave propagation to other sets of waves, which have generalized propagation invariant properties and finite energy. We capitalize again on the Laguerre-Gauss basis, to introduce self-imaging waves of finite energy, rotated self imaging, eigen-Fourier functions, all in a unified framework that includes rotating beams. For easy interpretation of these waves, we created the Gauss-Laguerre plane representation. Moreover, waves requiring infinite energy, which are based on paraxial Bessel functions, are obtained as a limiting case of Gauss-Laguerre functions.
Publications
- Yoav Y. Schechner and Joseph Shamir, “Parameterization and orbital angular momentum of anisotropic dislocations,” Journal of the Optical Society of America - A 13, pp. 967-973 (1996).
- Yoav Y. Schechner, Rafael Piestun and Joseph Shamir, “Wave propagation with rotating intensity distributions,” Physical Review E. 54, pp. R50-R53 (1996).
- Rafael Piestun, Yoav Y. Schechner and Joseph Shamir, “Self-imaging with finite energy,” Optics Letters 22, pp. 200-203 (1997).
- Rafael Piestun, Yoav Y. Schechner, and Joseph Shamir, “Propagation invariant wave-fields with finite energy,” Journal of the Optical Society of America A 17, pp. 294-303 (2000).
- Adam Greengard, Yoav Y. Schechner and Rafael Piestun, “Depth from rotating point spread functions,” Proc. SPIE: Optical Information Systems II (2004).
- Adam Greengard, Yoav Y. Schechner and Rafael Piestun, “Depth from diffracted rotation,” Optics Letters Vol. 31 , No. 2 , pp. 181-183 (2006).
Presentations
- “Rotating Beams” (1.2 Mb, PowerPoint)