Yoav Y. Schechner: Research

Focus-based Separation of Transparent Layers

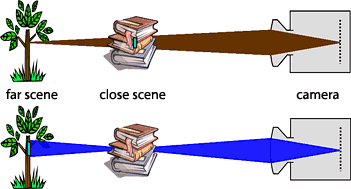
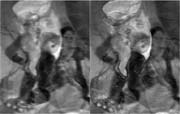
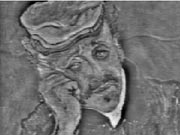
Consider situations where the depth at each point in the scene is multi-valued. This occurs when a virtual image is semi-reflected by a transparent surface. The semi-reflected image is linearly superimposed on the image of an object that is behind the transparent surface. Multi-valued depth exists also in microscopy and tomography. We study these cases.

The model of image formation is that of convolutive mixtures: when focusing on an object layer, the defocused layers are superimposed. We thus develop an approach for the separation of the superimposed layers. Focusing on either of the layers yields initial separation, but crosstalk remains. The separation is enhanced by mutual blurring of the perturbing components in the images. However, this blurring requires the estimation of the defocus blur kernels. We thus advocate self-calibration of the blur kernels, given the raw images. Hence, this is blind source separation (BSS) of convolutive image mixtures. In our earlier work, during the late '90s, we sought blur kernels that minimize the mutual information between the contents at different depths. Autofocusing and depth estimation in the presence of semi-reflections were also considered in this work.

Direct optimization of mutual information between convolutive signals is very complex and suffers from local minima. Thus, our recent work devises an efficient approach to solve these problems. The method is fast, while achieving high quality image separation. The convolutive BSS problem is converted into a set of instantaneous (pointwise) problems, using a short time Fourier transform (STFT). Standard BSS solutions for instantaneous problems suffer, however, from scale and permutation ambiguities. We overcome these ambiguities by exploiting a parametric model of the defocus point spread function. Moreover, we enhance the effiency of the approach by exploiting the sparsity of the STFT representation as a prior.

Publications

1. Yoav Y. Schechner, Nahum Kiryati and Ronen Basri, “Separation of transparent layers using focus,” International Journal of Computer Vision 89, pp. 25-39 (2000).
2. Yoav Y. Schechner, Nahum Kiryati and Joseph Shamir, “Blind recovery of transparent and semireflected scenes,” Proc. CVPR, Vol. 1, pp. 38-43 (2000).
3. Yoav Y. Schechner, Nahum Kiryati and Ronen Basri, “Separation of transparent layers using focus,” Proc. ICCV, pp. 1061-1066 (1998).
4. Yoav Y. Schechner, Nahum Kiryati and Joseph Shamir, “Multi-valued images and their separation,” Multi-Image Analysis, Lecture Notes on Computer Science Vol. 2032, pp. 129-141 (2000), Editors: R. Klette, T. Huang, and G. Gimel'farb.
5. Sarit Shwartz, Yoav Y. Schechner and Michael Zibulevsky, “Efficient separation of convolutive image mixtures,” Proc. ICA - Int. Conference on Independent Component Analysis and Blind Signal Separation, pp. 246-253 (2006).
6. Sarit Shwartz, Yoav Y. Schechner and Michael Zibulevsky, “Blind separation of convolutive image mixtures,” Neurocomputing, Vol. 71, pp. 2164-2179 (2008), Special issue on Advances in Blind Signal Processing.

Presentations

1. “Separation of Convolutive Image Mixtures” (6.2 Mb, PowerPoint)

Related Research

1. Separation of Semi-Reflections using Polarization Analysis
2. Depth from defocus vs. Stereo
3. Blind Source Separation