Software & Hardware
Software
Total Maximum Likelihood: An Alternative to Total Least-Squares
Amir Beck and Yonina C. Eldar
Total Maximum Likelihood
Estimation under uncertainty
conditions is an important problem in modern statistical signal processing. A
popular estimation problem is that of estimating an unknown, deterministic
vector parameter 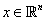 in
the linear model in
the linear model
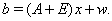 (1) (1)
Here 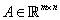 is a known model matrix,
while is a known model matrix,
while 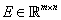 and and 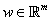 are
perturbations to the model matrix and the measurements, respectively. are
perturbations to the model matrix and the measurements, respectively.
The standard technique to
estimating 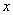 is
the total least-squares (TLS) method. In this approach, we seek the values of is
the total least-squares (TLS) method. In this approach, we seek the values of 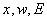 such that (1) is consistent, and the perturbations such that (1) is consistent, and the perturbations 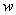 and and 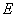 have minimal norm: have minimal norm:
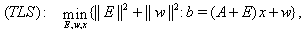
where for a matrix 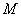 , the norm , the norm 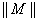 stands for the Frobenius norm. By minimizing with respect to stands for the Frobenius norm. By minimizing with respect to 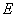 and and 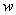 , the problem can be cast as the following minimization problem in , the problem can be cast as the following minimization problem in 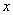 : :
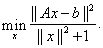 (2) (2)
Despite its popularity, in
practice, the performance of the TLS method can be quite poor. For example, in
the case when 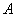 is
square and nonsingular, it does not take the uncertainty into account and
reduces to the conventional least-squares solution. In our work we propose a different
approach to estimating is
square and nonsingular, it does not take the uncertainty into account and
reduces to the conventional least-squares solution. In our work we propose a different
approach to estimating 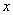 that has superior performance. The
motivation for this new method comes from a maximum likelihood (ML)
formulation, and is therefore referred to as the total ML (TML) estimate. that has superior performance. The
motivation for this new method comes from a maximum likelihood (ML)
formulation, and is therefore referred to as the total ML (TML) estimate.
To derive the TML estimate, we
assume that 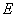 is
a matrix comprised of independent normal random variables with zero-mean and
variance is
a matrix comprised of independent normal random variables with zero-mean and
variance 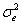 and
that and
that 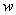 consists
of independent normal random variables with zero-mean and variance consists
of independent normal random variables with zero-mean and variance 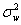 . We then estimate . We then estimate 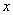 by computing the
ML solution under this model which amounts to solving: by computing the
ML solution under this model which amounts to solving:
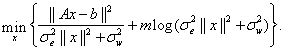 (3) (3)
Problem (3) can be solved efficiently by transforming it into a single-variable minimization of a unimodal function
[1,2].
The objective in (3) can be viewed as a regularization of the TLS problem (2). Therefore, this technique
provides statistical reasoning to regularized TLS and suggests an inherent
logarithmic penalty scheme. Statistical analysis carried out in [2], as well as
numerical simulations, demonstrate the superiority of the TML approach over
TLS. Despite its noncovenxity, the objective (3) can be minimized efficiently,
as detailed in [1,2].
Structured Total Maximum Likelihood
The TML technique can also be
extended to the case in which the model matrix 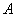 and consequently the perturbation
matrix and consequently the perturbation
matrix 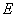 have
structure so that the perturbations are not arbitrary but rather follow a fixed
pattern. The resulting estimate is referred to as the structured TML (STML). As
with the TML, the STML can be viewed as a regularized version of the structured
TLS (STLS) approach in which the regularization consists of a logarithmic
penalty. However, in contrast to the STLS solution, the STML always exists.
Furthermore, its performance in practice tends to be superior to that of the
STLS. Methods to implement the STML efficiently are developed in [3]. have
structure so that the perturbations are not arbitrary but rather follow a fixed
pattern. The resulting estimate is referred to as the structured TML (STML). As
with the TML, the STML can be viewed as a regularized version of the structured
TLS (STLS) approach in which the regularization consists of a logarithmic
penalty. However, in contrast to the STLS solution, the STML always exists.
Furthermore, its performance in practice tends to be superior to that of the
STLS. Methods to implement the STML efficiently are developed in [3].
We treat the case in which 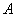 is known to have a
linear structure: is known to have a
linear structure:
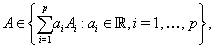
where 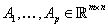 are the structure matrices
and are the structure matrices
and 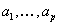 are
the structure components; typically are
the structure components; typically 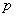 is smaller than is smaller than 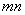 . This structure can be
taken into account in order to improve the estimation performance. Instead of
allowing . This structure can be
taken into account in order to improve the estimation performance. Instead of
allowing 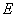 to
be an arbitrary matrix, we consider only structured perturbations of the form to
be an arbitrary matrix, we consider only structured perturbations of the form
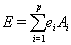
where  are the unknown
perturbation structure variables. are the unknown
perturbation structure variables.
The ML estimate of  in this case is
the solution to in this case is
the solution to
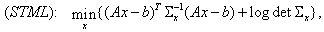 (4) (4)
where
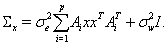
In [3] it is shown how to solve (4) efficiently in several special cases. In the Matlab package below we consider
solutions for arbitrary 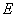 , as well as dedicated implementations
of two general classes of perturbations: , as well as dedicated implementations
of two general classes of perturbations:
1. In the first case, the perturbation matrix has the
form 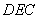 where where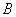 and and 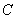 are given and are given and 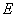 is arbitrary. For
example, the choice is arbitrary. For
example, the choice
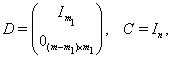
corresponds to the situation in
which the first 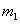 rows
of rows
of 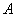 are
contaminated by noise, while the remainder are
contaminated by noise, while the remainder 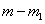 rows are noise free. The choice rows are noise free. The choice 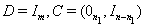 , corresponds to
the scenario in which the first , corresponds to
the scenario in which the first 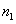 columns of columns of 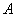 are error free while the
remaining are error free while the
remaining 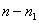 are
noisy. are
noisy.
2. In the second example, the perturbation 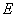 is a circulant
matrix. is a circulant
matrix.
In the figure below we illustrate
the behavior of the STML and STLS estimates. The problem is a discretization of
the famous Phillips test problem which is an integral equation of the first
kind.
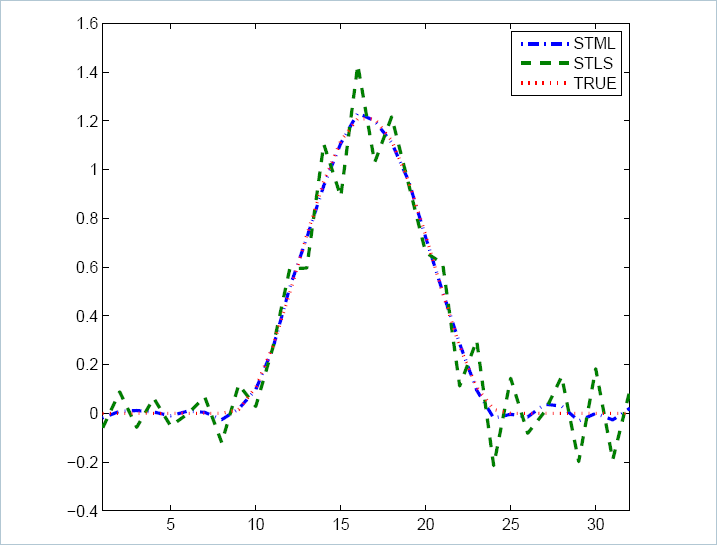
Evidently, The STML estimate
fits the true signal reasonably, while the STLS solution behaves erratically.
Reference
- A. Wiesel, Y. C. Eldar and A. Beck, "Maximum Likelihood Estimation in Linear Models with Gaussian Model Matrix", IEEE Signal
Processing Letters, vol. 13, no. 5, pp. 292-295, May 2006.
- A. Wiesel, Y. C. Eldar and A. Yeredor, "Linear Regression
with Gaussian Model Uncertainty: Algorithms and Bounds", IEEE Trans. on Signal Processing, vol. 56, no. 6, pp. 2194-2205, June 2008.
- A. Beck and Y. C. Eldar, "Structured Total Maximum Likelihood: An Alternative to Structured Total Least-Squares," SIAM. J. Matrix Anal. & Appl. Volume 31, Issue 5, pp. 2623-2649, Sept. 2010.
Software Download
- Download Total Maximum Likelihood Matlab Implementation.
Installation:
1. Unzip all files to a directory of your choice.
2. Update MATLAB's path to make the m-files of the package accessible.
3. Description of the package usage is available in the file guide.pdf.
|

