 |
Xampling
Pulse Streams, Multichannel
Multichannel Sampling of Pulse
Streams at the Rate of Innovation
Kfir Gedalyahu and Yonina C. Eldar
Introduction
We address
the problem of sampling signals which
are comprised of pulse streams. This model
is prevalent in applications such as
bio-imaging, neuronal activity and
ultra-wideband communication. Pulse
streams can viewed as parametric signals, which
are defined by the pulses delays and
amplitudes. Following this point of view, it was
suggested that the minimal sampling rate for
such a model, is the number of degrees of
freedom per unit of time, referred to as the rate
of innovation. Although sub-Nyquist schemes
for pulse streams were proposed in various
works, either the rate of innovation was not
achieved, or the pulse shape was limited to
Diracs. In addition, several of the methods are
unstable in the presence of noise.
In this work we present a new sub-Nyquist
architecture, which operate at the minimal sampling
rate, support general pulse shapes and exhibit high
noise robustness.
The model treated here is related to the one
used in the multipath medium
identification problem, however there are
two fundamental differences between the models,
which lead to different sampling strategies. The
first is that in contrast to the previous
setting, the unknown delays vary from period to
period.
Second, here we require that the pulses have
finite time support, and that pulses from one
period do not interfere with other periods.
Under this assumption, which is not required in
the previous model, each period of the signal
can be processed separately.
The advantages over the previous scheme is that it
supports varying delays from period to period, and
as we show next it requires a simpler digital
correction stage. The advantages of the previous
method are that it can treat pulses with infinite
time support and that it includes also single
channel configurations.
Signal Model
We consider a signal
comprised of an infinite number of delayed and weighted pulses.
It is assumed that in each time interval T there are L
pulses. Since each pulse is defined by 2 parameters - delay
and amplitude, in each interval there are 2L degrees of
freedom. Therefore the rate of innovation of the signal is 2L/T.
Our aim is to develop a sampling and reconstruction method
operating at this rate.
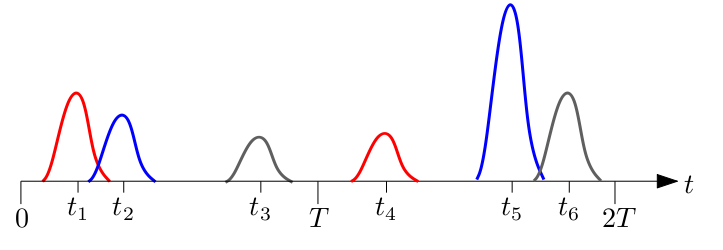
An example for stream of
pulses with L=2 pulses per period is given below:
X-ADC Scheme
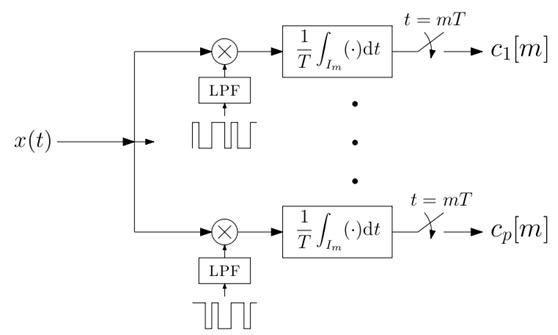
The sampling scheme is
comprised of p parallel sampling channels. In each
channel the input signal is modulated with a properly
designed waveform, followed by an integrator.
Various signals can be
used as modulating waveforms. Two useful examples are:
- Filtered
rectangular pulses modulated by ±1.
These waveform can be generated by the Modulated
Wideband Converter.
- Cosine and Sine
functions with multiples of a basic frequency of 1/T
(tones).
An example for a scheme based
on rectangular pulses as modulating waveforms:
Subspace Detection and Recovery Method
It was shown in [1] that each
sample at the output of the multichannel scheme, is
composed of a linear combination of the signal's Fourier
coefficients. By proper design of the modulating
waveforms, a set of 2L Fourier coefficients can be
extracted from the samples. Once the Fourier
coefficients are given the
unknown delays can be recovered using standard
methods for model-based complex sinusoids estimation,
such as the annihilating filter, matrix pencil
and more. See [1] for further details.
In order to perfectly recover the
delays and amplitudes, the number of sampling channels
has to be greater or equal to 2L, leading to a minimal
sampling rate of 2L/T. This rate equals to the signal's
rate of innovation, which is the minimal rate for such
models.
Performance in the Presence of Noise
We demonstrate the performance of our approach in
the presence of white Gaussian noise when working at the
rate of
innovation. We compare our results to those achieved by
the integrators and exponential filters based
methods.
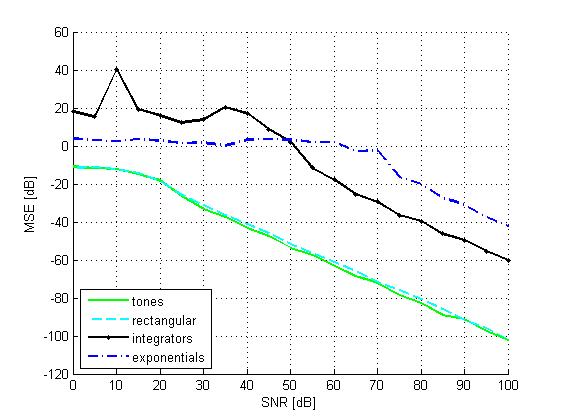
The MSE as function of SNR for L=2 Diracs per period and
sampling rate of 5/T is depicted below. The plot shows
that the two configurations supported by our scheme
(tones and rectangular pulses) outperform the previous methods.
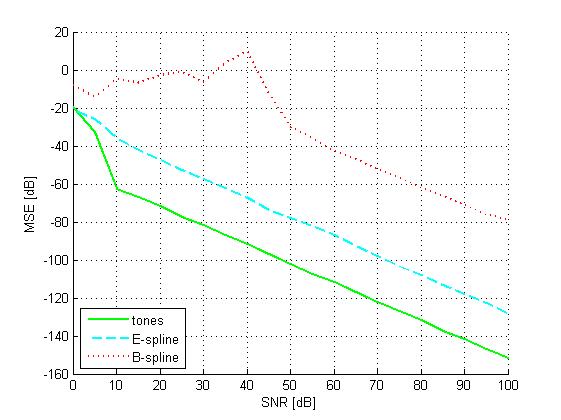
Next, we compare our method to the E-spline and B-splines
methods. These methods require a sampling rate of
64/T, for L=4 pulses per period. The results are shown
in the graph below. It can be shown that our approach is
also more robust than the ones based on splines, in
addition to its lower sampling rate requirement.
Reference
Software Download
Installation:
1. Unzip all files to a directory of your choice.
Usage:
1. Use MultiSampMix.m to perform sampling
of Diracs with the proposed method.
2. Use MultiRecoverMix.m to perform recovery of the Diracs delays from the samples,
where noise can be added to the samples prior to the recovery
stage.
3. For more information on the functions usage, see
MultiFRI.docx.
|
|

