 |
Xampling
Super-Resolution Radar
Introduction
Identification of time-varying linear systems, which introduce both time-shifts (delays) and frequency-shifts (Doppler-shifts), is a central task in many engineering applications such as radar. In this work we address the problem of identification of underspread linear systems (ULSs), defined as time-varying linear systems whose responses lie within a unit-area region in the delay--Doppler space, by probing them with a known input signal.
Classical results suggest that LTV systems can be identified as long as they are underspread, however this requires input signals with infinite time-bandwidth product. Recent results which relied on compressed sensing, do not provide super resolution estimation of the system's parameters and suffer from leakage effects.
The main contribution of this work is to characterize conditions on the bandwidth and temporal support of the input signal that ensure identification of ULSs described by a finite set of delays and Doppler-shifts from a single observation. By extending the scheme for multipath medium identification, we provide a procedure that enables identification of parametric ULSs from an input train of pulses in polynomial time.
In this work the Xampling methodology is used in order to achieve super resolution recovery of the delays and Dopplers, and to reduce the time-bandwidth product of the probing signal.
Problem Formulation
We address systems which described by a finite number of delays and Dopplers:
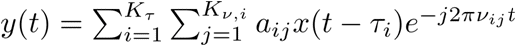
where aij is the complex attenuation factor associated with the delay-Doppler pair (ti,uij)
The ULS is probed with input signal consisting of a train of pulses:
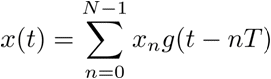
where xn is a known sequence and g(t) is a known pulse shape with bandwidth W and time support T.
We make the following assumptions:
1. The ULS is underspread - tmaxumax < 1
2. The maximal delay is smaller than T - tmax < T
3. The maximal Doppler shift is much smaller than W - umax<< W
Under these assumptions, the system output, can be written as:
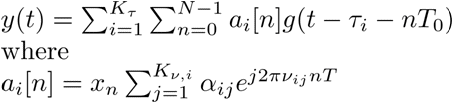
Our goal is to minimize the probing signal's time-bandwidth product, required in order to identify the system.
Main Result
The following result provide sufficient condition on the minimal time-bandwidth product if the input signal:

This result in different from the classical results of Kailtah (1962) and Bello (1963) which require require input signals with infinite bandwidth W and infinite time support T.
X-ADC Scheme
We use a similar scheme to the one used for the multipath medium identification. By applying this scheme on the on the signal y(t), we obtain the unknown delays ti and the sequences ai[n].
Then, in order to recover the Dopplers uij from the sequences ai[n], we use methods for parametric spectral estimation, such as annihilating filer or matrix-pencil.
When the pulses are confined to the period T we can use a simpler sampling and processing method referred to as Doppler focusing . This approach performs low rate sampling and digital processing of radar signals and enjoys an SNR improvement which scales linearly with N, obtaining good detection performance even at SNR as low as -25dB. This approach has been implemented in hardware; more details can be found on the hardware page.
Comparison with Other Methods
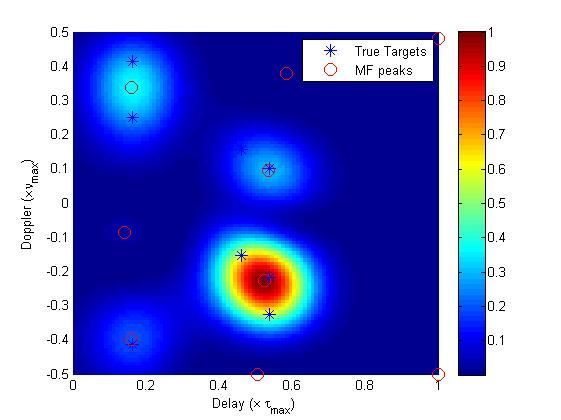
We start by comparing our result to those obtained by the classical matched-filtering (MF) approach. Our setup consists of 9 targets with maximal delays of 10 mirco seconds, and maximal Doppler of 10KHz. The probing signal used has a bandwidth of 1.2MHz and time duration of 0.48 mili seconds.
The results obtained by our method is shown in the following figure. It can be shown that all the targets have been perfectly recovered.
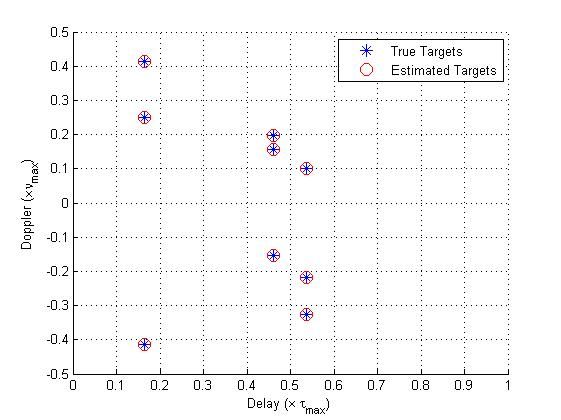
The recovery performed by the MF based approach is shown in the next figure. Clearly, this method has a limited resolution and it cannon distinguish between close targets in the Doppler-delay plane.
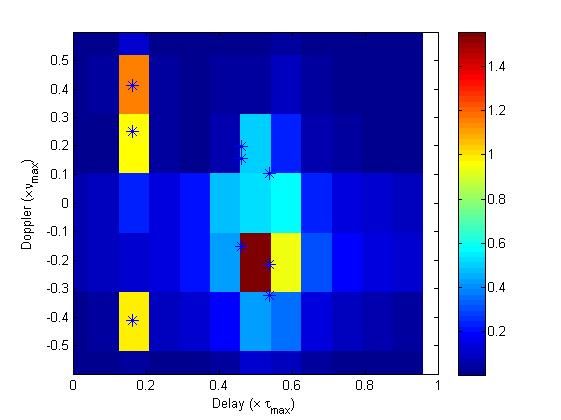
Next we investigates the results of compressed sensing based methods. These techniques do not attempt to recover the original ULS, but a discrete representation of it, which clearly has an inherit resolution limitation. Another major drawback of such works is that targets in the real-world do not in fact correspond to points in the quantized delay?Doppler space, which causes leakage of their energies in the quantized space. An example for a discrete representation of the discussed setup is shown in following figure:
Further comparisons and behavior in the presence of noise and clutter can be found here.
Reference
O. Bar-Ilan and Y. C. Eldar, "Sub-Nyquist Radar via Doppler Focusing",to appear in IEEE Transactions Signal Processing.
W. U. Bajwa, K. Gedalyahu and Y. C. Eldar, "Identification of Parametric Underspread Linear Systems and Super-Resolution Radar", IEEE Transactions on Signal Processing, vol. 59, no. 6, pp. 2548-2561, June 2011.
|
|

