 |
Software & Hardware
Software
CoRK: Optimal Phase Retrieval from 1D Fourier Measurements
K. Huang, Y. C. Eldar and N. D. Sidiropoulos
Introduction
We consider phase retrieval from the magnitude of 1D over-sampled Fourier measurements, a classical problem that has challenged researchers in various fields of science and engineering.
We show that an optimal vector in a least-squares sense can be found by solving a convex problem, thus establishing a hidden convexity in Fourier phase retrieval. We then show that the
standard semidefinite relaxation approach yields the optimal cost function value (albeit not necessarily an optimal solution). A method is then derived to retrieve an optimal minimum phase
solution in polynomial time. Using these results, a new measuring technique is proposed which guarantees uniqueness of the solution, along with an efficient algorithm that can solve large-scale
Fourier phase retrieval problems with uniqueness and optimality guarantees. The proposed method is termed auto-correlation retrieval – Kolmogorov (CoRK).
Main Idea
We start with the least-squares formulation for 1D Fourier phase retrieval
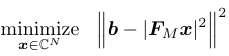 where FM denotes first N columns of the M-point DFT matrix. Due to the special structure of the DFT matrix, we show that this seemingly non-convex problem is exactly equivalent to the following convex problem
where FM denotes first N columns of the M-point DFT matrix. Due to the special structure of the DFT matrix, we show that this seemingly non-convex problem is exactly equivalent to the following convex problem
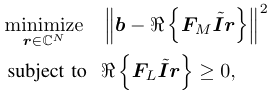 where FL denotes first N columns of the L-point DFT matrix with a sufficiently large L. The constraint ensures that r is an auto-correlation sequence, which we assumed to be the auto-correlation of x.
To retrieve a solution x from r, we can simply invoke spectral factorization, which is a relatively well-studied subject, and we do it via Kolmogorov’s method.
where FL denotes first N columns of the L-point DFT matrix with a sufficiently large L. The constraint ensures that r is an auto-correlation sequence, which we assumed to be the auto-correlation of x.
To retrieve a solution x from r, we can simply invoke spectral factorization, which is a relatively well-studied subject, and we do it via Kolmogorov’s method.
Given the Fourier intensity of a signal s, |FMs|2, there are many alternative solutions of s that gives the same Fourier intensity, besides a global phase shift, spatial shift, and conjugate reversal.
The solution given by spectral factorization has the property of minimum phase, which is not a natural assumption to make for the signals that we want to estimate.
Our idea then is to construct a minimum phase signal before measuring its Fourier intensities, so that it can be uniquely identified via 1D Fourier phase retrieval.
The procedure is very simple: For an arbitrary complex signal s, the augmented signal [δ; s] is minimum phase if |δ|>||s||1.
Summary of the Method
- Construct a minimum phase signal [δ; s] and then measure its Fourier intensity.
- Apply CoRK as follows:
- Solve the convex quadratic programming with respect to r, the auto-correlation of the signal, using ADMM;
- Extract the minimum phase solution using Kolmogorov’s method.
- Obtain an estimate by deleting the first element of the solution.
CoRK only does the second step, i.e., solves the problem optimally and produces a minimum phase solution. However, to retrieval the signal accurately, it is recommended to perform the first and third steps.
An Illustrative Example
In each Monte-Carlo trial, we first set N as a random integer between [1,1024], and then choose M as the smallest power of 2 that is larger than 4N.
A random signal 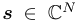 is then generated with elements drawn from i.i.d. is then generated with elements drawn from i.i.d. 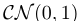 .
Two kinds of measurements are collected for performance comparison: directly measure .
Two kinds of measurements are collected for performance comparison: directly measure 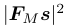 , and construct a minimum phase
signal smin with δ=3N then measure , and construct a minimum phase
signal smin with δ=3N then measure 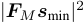 . We compare CoRK with the classical Fienup’s algorithm,
possibly also followed by spectral factorization if we know the measured signal is minimum phase. The reconstruction error (after resolving global phase ambiguity) and time consumed are shown in the following figures. . We compare CoRK with the classical Fienup’s algorithm,
possibly also followed by spectral factorization if we know the measured signal is minimum phase. The reconstruction error (after resolving global phase ambiguity) and time consumed are shown in the following figures.
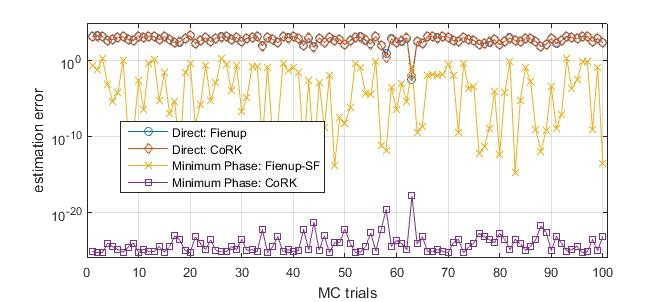
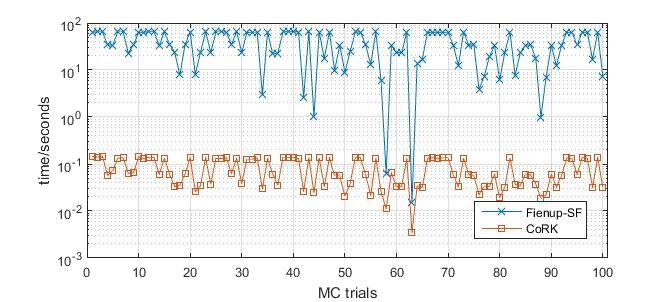
References
Software Download
The simulator is freely available for download and manipulation for academic use only, under the GNU license.
Installation:
1. Unzip.
2. Follow the instructions in the ReadMe.txt
|
|

