Software & Hardware
Software
Sparse Signal Recovery with the Boltzmann Machine Model
Tomer Faktor , Yonina C. Eldar , Michael Elad
Overview
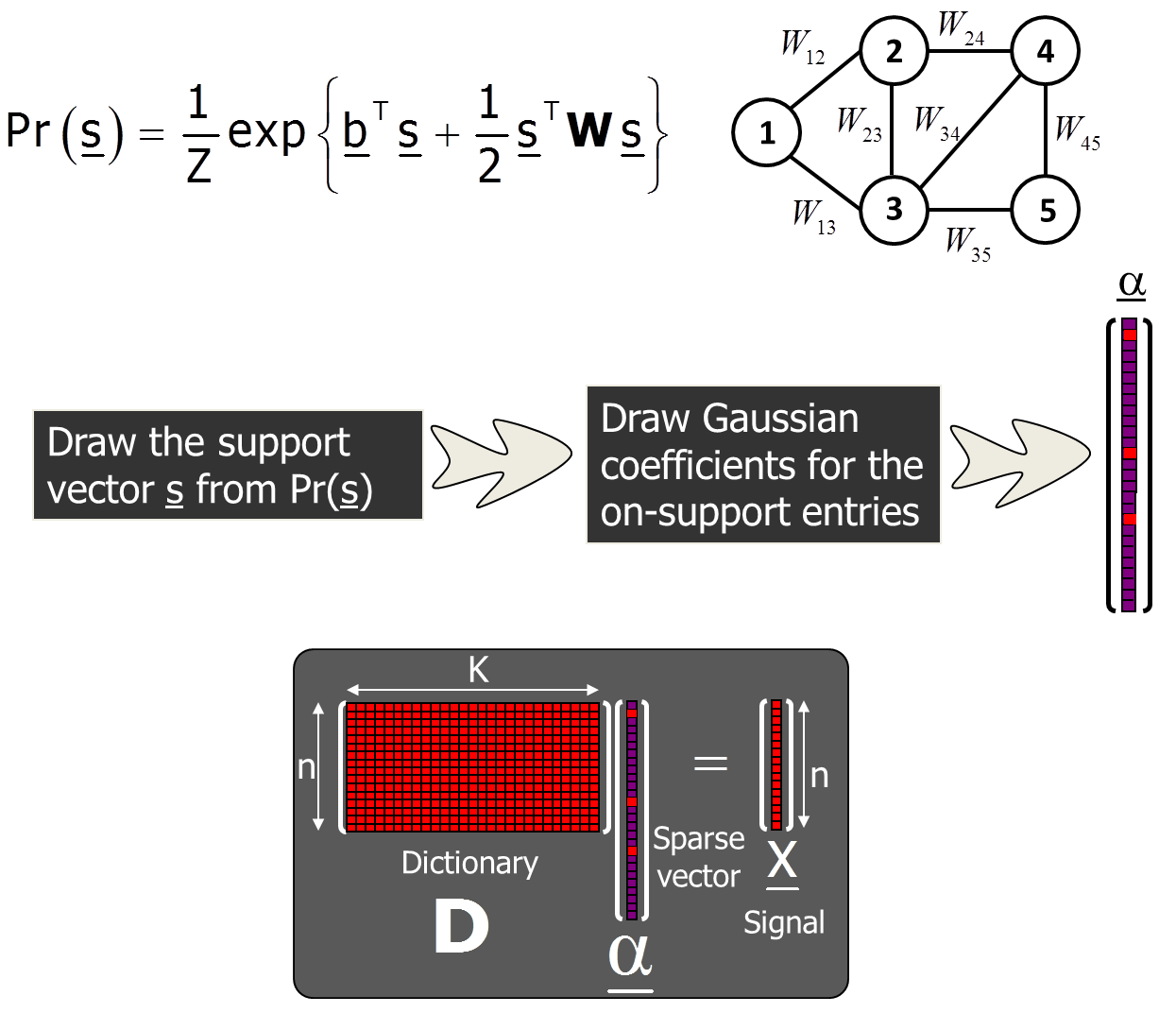
In the classical sparsity model the signal is assumed to be generated as a linear combination
of a few atoms from a given dictionary. However, in many setups assuming sparsity alone does not
suffice and exploiting prior knowledge on the sparsity pattern can improve the quality of sparse recovery.
This extension is regarded to as structured sparsity models and aims at going beyond the classical assumption
of independence between the entries of the sparsity pattern.
We focus on a statistical model that takes into account dependencies between the dictionary atoms and show how
this model can be used for sparse signal recovery. We follow the suggestion of several recent works (see the paper
for more details) and model the sparsity pattern by a Boltzmann machine (BM), a commonly used graphical model.
The parameters of this model are a bias vector and an interaction matrix.
BM-based Sparse Recovery
Pursuit of the sparse representations using the BM model is based on a Bayesian design (MAP\MMSE).
The Bayesian estimators are approximated using greedy or random approaches.
In the special case of a unitary dictionary and a banded interaction matrix the exact MAP estimator is
computed using message-passing techniques.
The learning of the Boltzmann parameters is based on a maximum pseudo-likelihood (MPL) approach.
The MPL is a convex optimization problem and we solve it using the sequential subspace optimization (SESOP) method.
Joint pursuit and model update are performed using a block-coordinate relaxation approach, resulting in an adaptive BM-based
sparse recovery scheme.
The effectiveness of our proposed approach is demonstrated both on synthetic data and image patches. Some example results
for the Boltzmann parameters learned for image patches represented over the unitary DCT dictionary are shown below.

The following BMBox package contains all our Matlab code to reproduce the results of the reference below.
Reference
Software Download
Usage:
Several examples of using the pursuit algorithms on synthetic data can be found in test_BM_unitary_pursuit.m and test_BM_redundant_pursuit.m, which generates Figures 4 and 5 in the reference. An example of learning the Boltzmann parameters for synthetic data appears in test_BM_learning.m which reproduces Figure 6 in the reference. Finally, an example of using the adaptive BM-based denoising scheme on image patches is given in test_BM_denoising_patches.m.
|

