Visualizing Image Priors
ECCV 2016
Tamar Rott Shaham
Tomer Michaeli
Technion
- Israel Institute of Technology
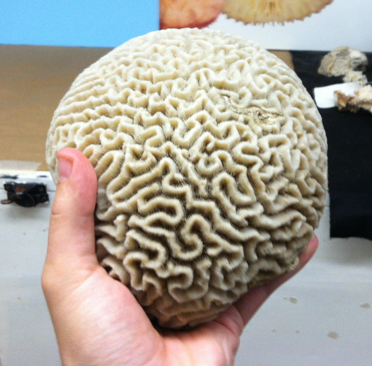
Our algorithm determines how images should be deformed so as to better comply with a given image model (exemplified here on a Brain Coral image). The deformed images give insight into the elementary geometric features to which the prior resonates. As can be seen, different image models (BM3D, EPLL, FoE, KSVD, Multi-Layer Perceptron, Nonlocal means, Total Variation, Shrinkage Fields with pairwise cliques) have quite different geometric preferences.
Abstract
Image priors play a key role in low-level vision
tasks. Over the years, many priors have been proposed, based on a wide variety
of principles. While different priors capture different geometric properties,
there is currently no unified approach to interpreting and comparing priors of
different nature. This limits our ability to analyze failures or successes of
image models in specific settings, and to identify potential improvements. In
this paper, we introduce a simple technique for visualizing image priors. Our
method determines how images should be deformed so as to best conform to a
given image model. The deformed images constructed this way, highlight the
elementary geometric structures to which the prior resonates. We use our
approach to study various popular image models, and reveal interesting
behaviors, which were not noticed in the past. We confirm our findings through denoising experiments. These validate that the structures
we reveal as ‘optimal’ for a specific prior are indeed better denoised by this prior.
Visual Comparisons
We used our algorithm to visualize several different natural image models by generating their GEMs. The GEM image stress out which spatial image features are more plausible under a given prior model. As can be seen, different models have quite different geometric preferences.
Downloads
Matlab Code - You can visualize your own Prior!