|

|
Theoretical Background
The method was first introduced by Yael Pritch
et al and is protected
by US patent – 20100232729.
|
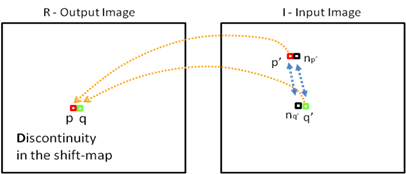
Shift-Map
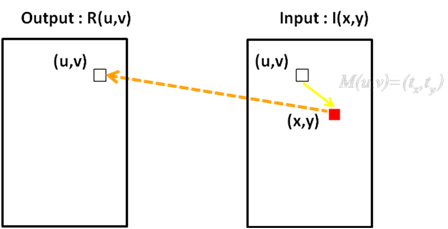
Shift-Maps represent a mapping for each pixel in the output image
into the input image. Using the following relations:
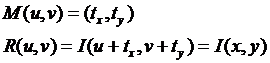
I – Input image
R – Output image
M – Shift-Map
The shifts are calculated separately for the two axes and each
pixel in
the result image is originated from the appropriate pixel in the input.
| Energy Minimization
Finding the optimal mapping can be described as an energy
minimization problem:
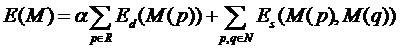
Where Ed represents external editing requirements (data term)
and Es assigns penalty to discontinuities introduced in the ouput image and avoids stitching artifacts.
the problem is solved using a graph labeling
algorithm and the labels are translated to shifts.
| Inpainting data term
Inpainting data term
uses data mask D(x,y) over
the input image. The mask is obtained by the user and represents the parts
in the input image that should be forced not to be included in the output
image.
We set D(x,y)
= ∞ for pixels
to be removed and D(x,y) = 0 elsewhere.
For each output pixel P = (u,v) and
M(u,v):
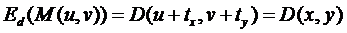
| Smoothness term
The smoothness term assigns a penalty to a discontinuity
introduced to the output image by a discontinuity in the Shift-Map. This
term should minimize editing artifacts and create good stitching in the
output image.
The discontinuities are computed based on color and gradient
differences (preserve image structure) using the following formula:
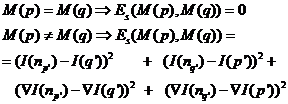
| Graph labeling
We used the α-expansion algorithm implemented by Olga Veksler et al. More details can be found in the final
project report.
| Hierarchical solution
Optimal solution for the graph labeling problem might be very
complicated. However hierarchical approach for graph
labeling problems were proposed in some recent works in computer
vision and can be used in this problem as well.
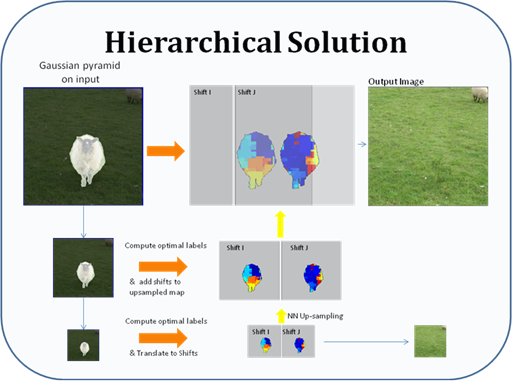
The solution is based on Gaussian pyramid.
first we reduce the image size to about 100X100
pixels. We calculate the optimal solution for the small image and translate
it to shifts. In the next step we use Nearest-Neighbor technique in order
to up-sample the resulting shift map and add a coarse solution for the map
(calculating shift for the larger image with only 8 moves for each pixel).
The process continues until we get the full size result.
|