Xampling
Sequences of Innovation
Multipath Medium Identification
Using Efficient Sampling Schemes
Kfir Gedalyahu and Yonina C. Eldar
Introduction
The problem of time delay estimation
arises in many applications in which a multipath medium
has to be identified using pulses transmitted through
the medium. Various approaches have been proposed in the
literature to identify the delays introduced by the
multipath environment, however these methods require
high sampling rates in order to achieve reasonable time
resolution. In
this work we present a new method, allowing the recovery
of the medium parameters from sub-Nyquist samples. Our
approach can identify a medium comprised of L
propagation paths, by sampling its output at a rate of
2L/T, irrespective of the pulse bandwidth.
Signal Model
The medium is
assumed to be probed with a known pulse at a constant
rate of 1/T. The received signal from the medium is
comprised of L pulses per period, corresponding to L
propagation paths. The delays in each period are assumed
to be constant, where the reflection coefficients of the
pulses can vary from period to period. There is no
constraint on the pulses support, and they can have
infinite time support.
Mathematically such a model is defined as
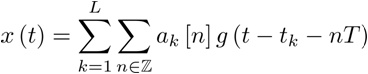
where ak[n] and tk are the reflection
coefficient and delay of the kth propagation
path, and g(t) is the pulse shape.
An example of a received signal from a medium with L=2
propagation paths is given below:
Another possible application for such signal model is high-resolution radar.
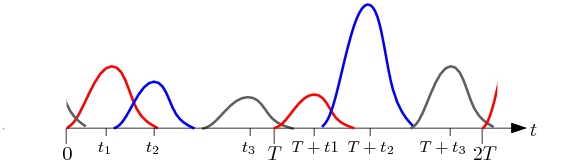
Xampling System
The proposed method is comprised of three main stages:
1. Sampling stage:
The input signal is sampled using p
parallel sampling channels. Each channel consists of a sampling filter si(t), followed by a
uniform sampler operating at a rate of 1/T. The
number of sampling channels has to be greater or
equal 2L, leading to an average sampling rate
of 2L/T.
Examples of filters selections:
- A set of 2L ideal complex
band-pass filters, each one covering a different
frequency band of width 1/T.
- Low pass
filter with a width of 2L/T, followed by a
uniform sampler operating at a rate of 2L/T.
In this case the parallel sampling sequences
are obtained by a serial to parallel
converter, as we will show next.
2. Equalization stage:
The sampling sequences at the output of the
sampling stage are filtered using a properly
designed digital filter-bank
W-1(ejwT) (see [1] for
details).
3. Reconstruction stage:
After the equalization stage the delays are
recovered from the samples at the output of the
digital filter-bank the using the well known
ESPRIT algorithm. Then, the reflection
coefficients are recovered using additional
digital filter-bank.
The full sampling and reconstruction scheme is given below
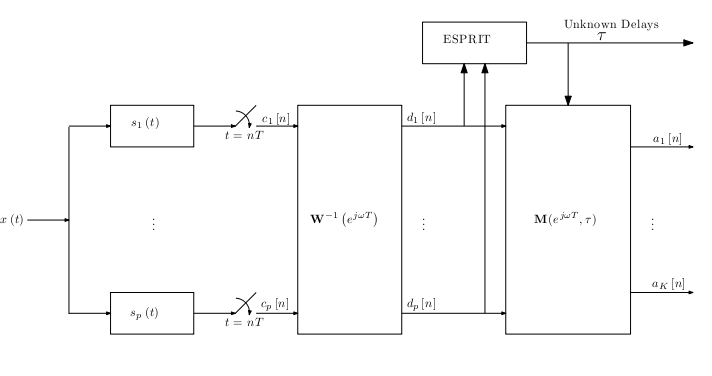
One special case of the proposed scheme, is when only
one physical sampling channel is used. In this case a
low-pass filter is used as a sampling kernel, followed
by a uniform sampler at a rate of 2L/T. The parallel
sampling sequences are obtained using a
serial-to-parallel device. Moreover, it can be shown
that in this case the first digital correction filter
bank, can be decomposed into three stages: two stages of
parallel one-dimensional filters Ψi(ejwT) and Φi(ejwT) and FFT operation.
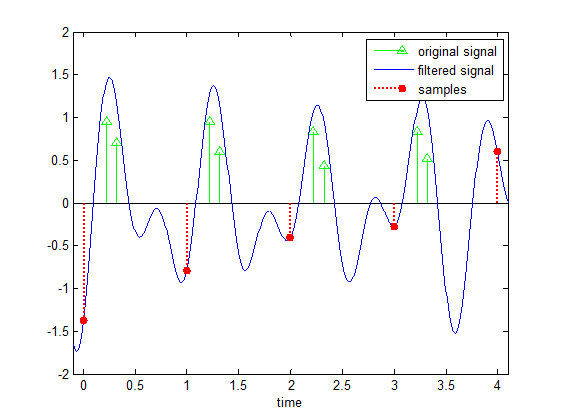
We now provide an example demonstrating the
importance of the sampling filter. We consider the case
where the input signal is comprised of L=2 Diracs per
period. In the following figure, we show the output of
one of the sampling channels. This example demonstrates
the need for the sampling kernel when sampling
short-length pulses at a low
sampling rate. The sampling kernels have the effect of
smoothing the short pulses (Diracs in this example).
Consequently, even when the sampling rate is low, the
samples contain information about the signal. In
contrast, if we were to sample the input signal directly
at a low rate, then we would often obtain only zero
samples which contain no information about
the signal.
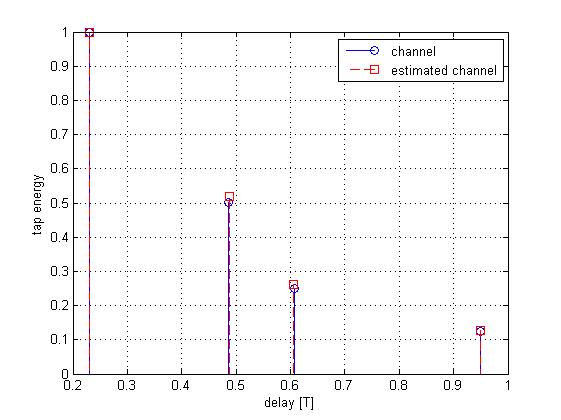
Channel Identification Example
An example for identification of a multipath channel is
depicted below. The channel consists of L=4 propagation
paths. The medium is assumed to be probed with Diracs at a
rate of 1/T. The recovery of the medium parameters is performed from noisy samples with SNR of 10dB taken at a rate of 8/T.
The original and estimated delays and average energy of each
propagation path are shown in the figure. Our method provides good estimation of the channel
parameters. In contrast, in this setting sampling at the
Nyquist rate is inapplicable since the pulses are not
band-limited.
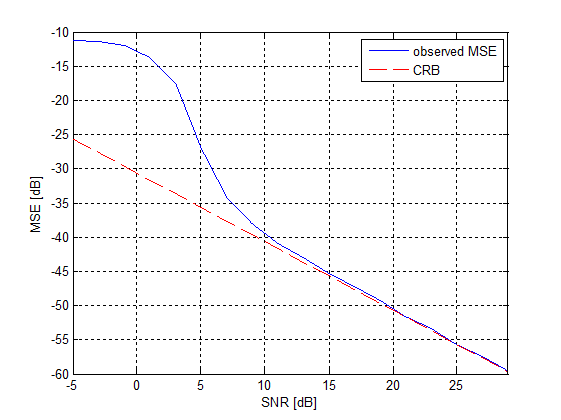
Next, we explore the performance of our method in the
presence of noise, for the above channel setting. The MSE of
the delays estimation is plotted as a function of the samples
SNR. It can be seen that for SNR above 10dB, our method
achieves the Cramer-Rao bound (CRB).
Reference
Software Download
Installation:
Unzip all files to a directory of your choice.
Usage:
Run LRTDE.m. Instructions on the GUI operation can be found
in LRTDE_GUI.docx.
Installation:
Unzip all files to a directory of your choice.
Usage:
Use AnalogSampling.m to perform sampling of a multipath channel ouput.
Use ChanRecover.m to perform recovery of the channel's
parameters. For more information on the functions usage see
LRTDE_Package.docx.
|

