Software & Hardware
Software
Sparse and low-rank decomposition, also known as robust principle component analysis has been applied successfully in numerous applications.
Typically, this approach leads to a minimization problem which is solved using iterative algorithms.
Drawing inspiration from recurrent networks, in recent years deep-learning strategies have been extended to mimic the behavior of iterative algorithms, with reduced complexity.
In this work, we propose an extension of these deep architectures to robust principle component analysis in which fully connected layers are replaced with convolutional ones.
This strategy offers spatial invariance and significant reduction in the number of learned parameters.
We then apply the proposed method to contrast enhanced ultrasound, in which low-rank tissue signal is ought to be removed to visualize blood vessels.
We demonstrate the effectiveness of our approach on simulations and in-vivo rat brain scans.
The resulting images exhibit improved visual quality and contrast compared with images obtained by commonly practiced methods.
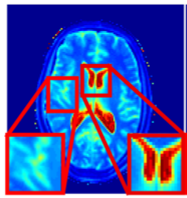
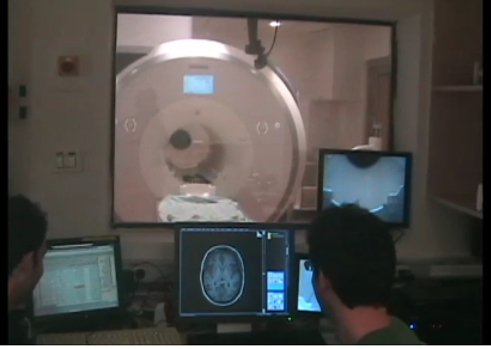
In this work, we introduce a new approach for quantitative MRI using MRF, called Magnetic Resonance Fingerprinting with Low Rank (FLOR).
We exploit the low rank property of the concatenated imaging constrasts, on top of the fact that the MRF signal is sparsely represented in the generated dictionary domain.
We present an iterative scheme based on the proximal gradient method, which consists of a gradientstep followed by a low rank projection using the singular value decomposition.
Experiments on real MRI data, acquired using a spirally-sampled MRF FISP sequence, demonstrate better resolution compared to other compressed-sensing based method for MRF.
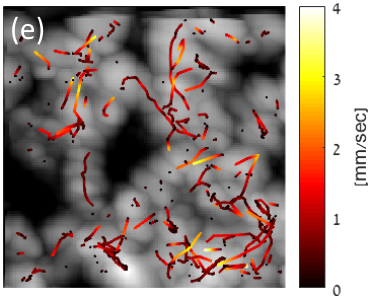
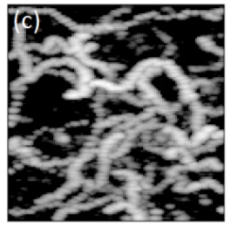
Ultrasound localization microscopy offers new radiation-free diagnostic tools for vascular imaging deep within the tissue.
Despite its high spatial resolution, low microbubble concentrations dictate the acquisition of tens of thousands of images, over the course of several seconds to tens of seconds, to produce a single super-resolved image.
To address this limitation, sparsity-based approaches have recently been proposed to significantly reduce the total acquisition time, by resolving the vasculature in settings with considerable microbubble overlap.
Here, we report on initial results of improving the spatial resolution and visual vascular reconstruction quality of sparsity-based super-resolution ultrasound imaging from low frame-rate acquisitions, by exploiting the inherent kinematics of microbubbles' flow.
Our method relies on simultaneous tracking and sparsity-based detection of individual microbubbles.
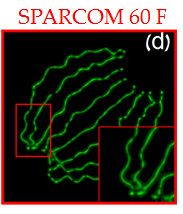
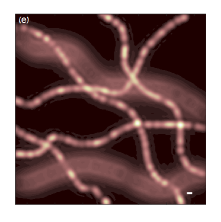
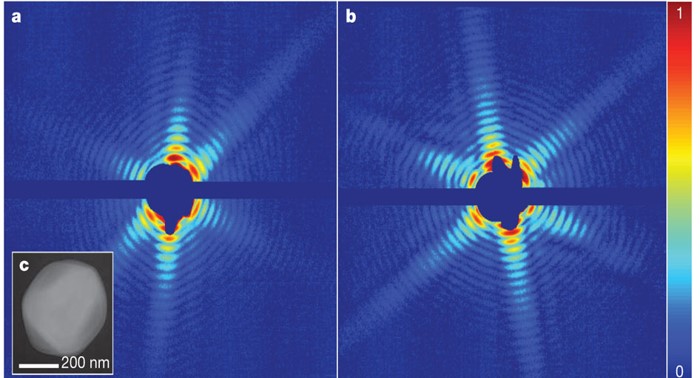
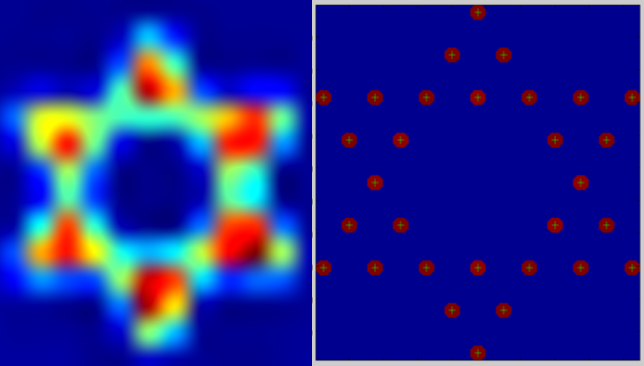
We present a new method for super-resolution in fluorescence microscopy, "sparsity-based super-resolution correlation microscopy" (SPARCOM).
SPARCOM exploits sparsity in the correlation domain to dramatically reduce the number of required frames to produce a single super-resolved image.
SPARCOM achieves spatial-resolution comparable to single-molecule techniques, while maintaining short integration time.
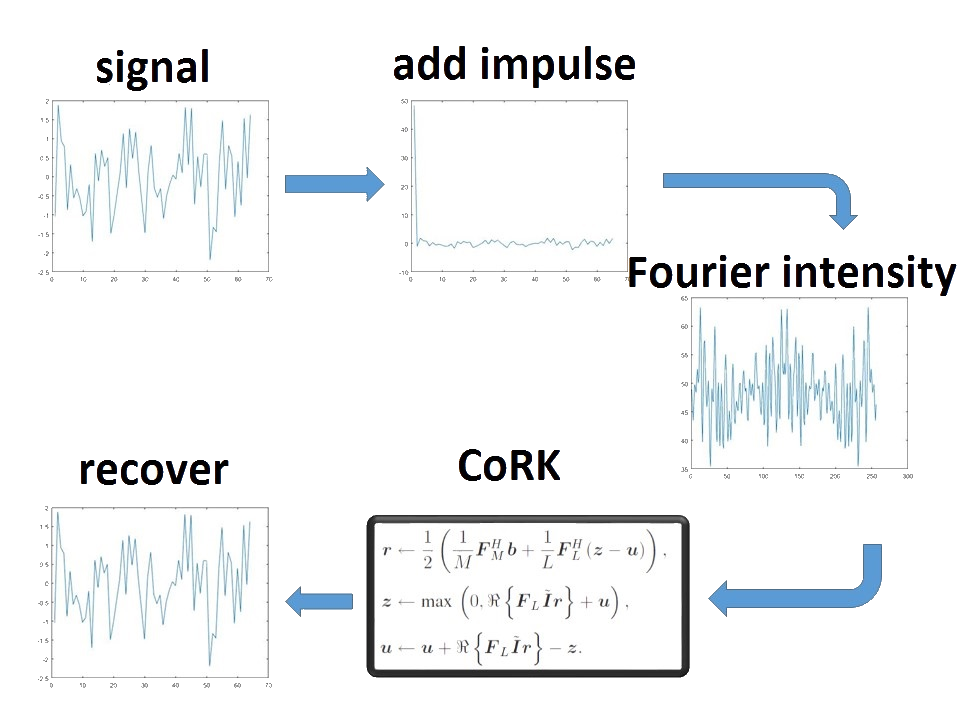
The proposed method, termed auto-correlation retrieval -- Kolmogorov (CoRK), optimally solves the 1D Fourier phase retrieval problem.
The phase retrieval problem is first equivalently reformulated with respect to the auto-correlation of the signal, resulting in a convex quadratic programming problem.
An ADMM algorithm is then designed to efficiently solve this problem. Finally, a solution is extracted from the auto-correlation using Kolmogorov's algorithm, which has the property of minimum phase.
To ensure uniqueness of the solution, we add an impulse to the signal, with magnitude larger than the ℓ1 norm of the signal, before measuring the Fourier intensities.
We present a MATLAB based simulation tool for the acquisition process of a movie of fluctuating emitters with varying densities in an epi-fluorescence optical microscope. The simulator encompasses the physical aspects of the data acquisition process, including sample geometry, diffraction of light, camera quantization effects and noise. The simulator can be operated using a user friendly GUI or directly from the MATLAB command line, and is configurable via a simple text file.
We propose a gradient descent algorithm to recover a signal from its phaseless STFT measurements. The algorithm is initialized by the principle eigenvector, with proper normalization, of a designed matrix. This matrix is constructed as the solution of a simple least-squares problem. In contrast to previous works, the algorithm is computationally efficient, stable in the presence of noise and enjoys theoretical guarantees.
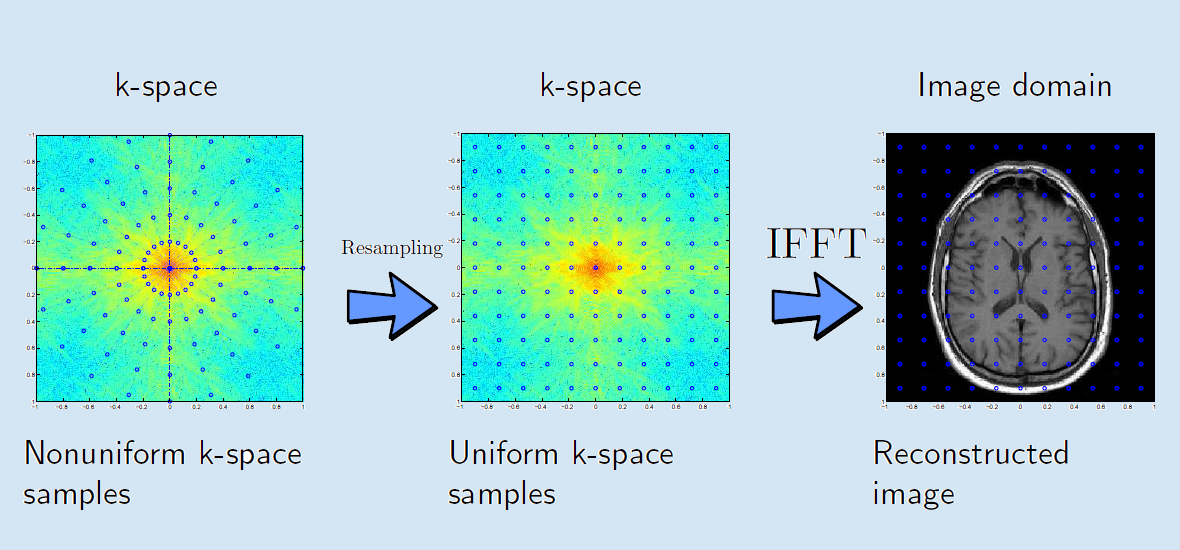
We present an algorithm for resampling a function from its values on a non-Cartesian grid onto a Cartesian grid. This problem arises in many applications such as MRI, CT, radio astronomy and geophysics. Our algorithm, termed SParse Uniform ReSampling (SPURS), employs methods from modern sampling theory to achieve a small approximation error while maintaining low computational cost.
We propose an adaptive MRI reconstruction approach from undersampled MRI measurement. Our general framework utilizes a reference image that exists in many MRI imaging scenarios. This reference can take on different forms: different imaging contrasts as done routinely in MRI acquisition, adjacent slices, or prior scans of the same patient. Our software package consists of examples of using this prior information in a compressed sensing framework, where the validity of the reference scan is determined during reconstruction in an adaptive fashion.
We extend the ideas of compressed sensing to general nonlinear measurement models. More specifically, we provide a software package to treat the problem of minimizing a general continuously differentiable function subject to sparsity constraints. Our algorithms are based on the notions of stationarity and coordinate-wise optimality. We present three algorithms: iterative hard thresholding, greedy and partial sparse-simplex methods. The latter two methods are generalization of orthogonal matching pursuit to the nonlinear setting.
We propose GESPAR (GrEedy Sparse PhAse Retrieval): An efficient method for phase retrieval of sparse signals, with good recovery performance. Our algorithm is based on a fast 2-opt local search method applied to a sparsity constrained non-linear optimization formulation of the problem. In essence, GESPAR is a local-search method, where the support of the sought signal is updated iteratively, according to certain selection rules. A local minimum of the objective function is then found given the current support using the damped Gauss Newton algorithm. GESPAR is fast, and is shown to lead to superior performance over Fienup and SDP based methods.
A 1-D piecewise constant segmentation method, based on wavelet decomposition and thresholding, which detects significant breakpoints in the data.Over 1,000 times faster than leading approaches, with similar performance.

Simulation package of sub-Nyquist sampling and support recovery using the modulated wideband converter (MWC). This page describes the MWC design, the Matlab code, and offers two software packages: analog and digital versions. The former simulates the samples that would have been obtained by true hardware. The latter provides a digital approximation of the MWC. The analog simulations consume more time but are more accurate.
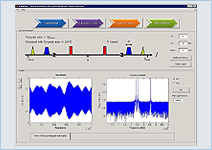
A GUI package written in Matlab that provides a user-friendly introduction of the MWC. The GUI environment guides the user through 4 steps: building a multiband model, configuring the MWC and sub-Nyquist sampling, support recovery using the continuous-to-finite (CTF) block, and finally continuous reconstruction.
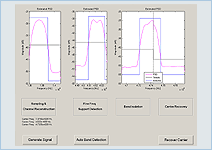
The modulated wideband converter (MWC) enables sub-Nyquist sampling of narrowband transmissions, when their carrier frequencies are unknown to the sampler. Reconstruction from the MWC sub-Nyquist samples is demonstrated in the package above. This GUI package provides signal processing of the narrowband transmissions by estimating the carrier frequencies from the lowrate samples. It also recovers the information bits that are encoded in the narrowband transmission of interest. 
The fundamental principle underlying compressed sensing is that a signal, which is sparse under some basis representation, can be recovered from a small number of linear measurements. However, prior knowledge of the sparsity basis is essential for the recovery process. Blind compressed sensing (BCS) avoids the need to know the sparsity basis in both the sampling and the recovery process under suitable conditions. This webpage explains the fundamentals of BCS and provides software for solving certain cases of the BCS framework.
Blind minimax estimation (BME) is a biased estimation technique for the linear regression problem, which provably dominates the ordinary least-squares approach. In other words, BME always achieves lower mean-squared error than least-squares. This web page contains a friendly introduction to BME as well as downloadable Matlab files implementing the BME algorithms.
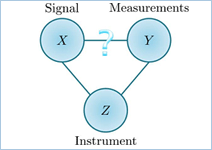
Bayesian estimation techniques require knowledge of the statistical relation between the desired signal and the measurements. In many practical scenarios, however, this relation is not fully known. This software implements our instrumental variable approach for treating such situations, which is based on a worst-case design strategy.
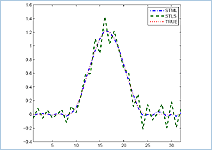
We describe an alternative to the popular total least-squares (TLS) method for solving linear systems of equations with uncertainty in the model matrix. This approach, referred to as total maximum-likelihood (TML), is based on maximum-likelihood optimization. Statistical analysis, as well as numerical simulations, demonstrate the superiority of the TML approach over TLS. We describe the TML method and provide a software package for evaluating the TML estimate under a broad set of conditions.
FIA (Fluxomers Iterative Algorithm) is an open-source software for analysis of 13c metabolic tracer experiments.
The software is based upon Fluxomers, a new set of variables resulting with a very efficient investigation of complex metabolic networks.
The software supports the 13CFLUX software FTBL input file format, as well as its new (but very similar) textual FIA declaration input file.
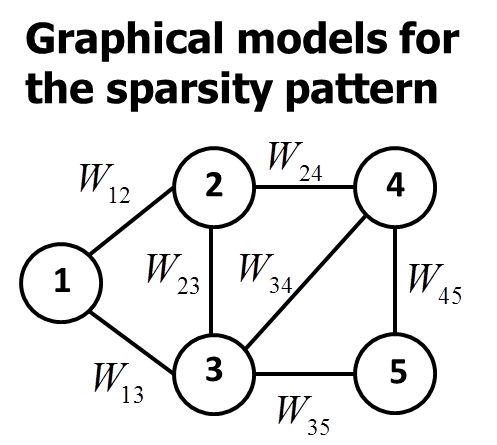
Structured sparsity models like block-sparsity and wavelet trees have drawn considerable
attention in recent years. A general framework for capturing dependencies between dictionary atoms is achieved by a
statistical model that is based on a Boltzmann machine (BM) prior on the sparsity pattern. The BM-based framework allows
us to revisit the sparse recovery problem. This webpage explains the fundamentals of the BM-based model and sparse recovery,
and provides downloadable Matlab files implementing the BM-based algorithms.
|

