 |
Software & Hardware
Software
Bayesian Estimation with Partial Knowledge
Tomer Michaeli and Yonina C. Eldar
Overview
A common problem in signal processing is to recover a signal x from measurements y. Examples include image denoising and deblurring, speech enhancement and dereverberation, target tracking and more. Situations of this type are often tackled by employing Bayesian estimation techniques such as the minimum mean-squared error (MMSE), linear MMSE (LMMSE) and maximum a posteriori (MAP) estimators. The Bayesian framework relies on the assumption that x is a random quantity drawn from some prior probability density function fX(x) and that the statistical relation between y and x is characterized by a likelihood function fY|X(y|x).
The prior fX(x) can typically be learned from a set of examples of clean signals. Indeed, a large variety of databases of all kinds of signals are available online, including facial images, fingerprints, iris scans and speech signals to name a few. The likelihood fY|X(y|x), on the other hand, is associated with the degradation mechanism in a specific application and thus cannot be learned from databases of this sort. One possibility for obtaining fY|X(y|x) is to assume a known degradation model such as additive white Gaussian noise. However, in many situations this assumption is over-simplistic since the degradation includes complicated effects, which are hard to model and sometimes not even known. Nonlinear distortion in CCD sensors, unknown blur and signal dependent noise are a few examples of such phenomena. An alternative approach for obtaining fY|X(y|x) is to learn it by collecting a paired set of examples of clean and degraded signals. Unfortunately, constructing such a database requires a complicated experimental setting in which our sensor is co-calibrated with some high-quality sensor, and is therefore usually impractical. Specifically, it is typically quite simple to obtain a set of clean signals from some a high-grade sensor (or from an existing database). Similarly, it is also easy to collect a set of degraded signals taken with our low-grade sensor. But these two sets are unpaired.
How can we estimate x from y without knowing the degradation model? The answer is simple – employ an instrument z. An instrument is a random quantity whose statistical relations with x and y are known or can be learned from examples. Consider, for instance, the task of enhancing a video sequence y of a speaker taken from a low-quality cellular-phone camera. In this case we can use the audio z as an instrument. Clearly, we can collect paired examples {yn,zn} of the noisy video and its associated audio (taken with the cellular-phone), as well as paired examples {xn,zn} of clean video sequences with their audio (taken from a high-quality camcorder), as schematically shown below.
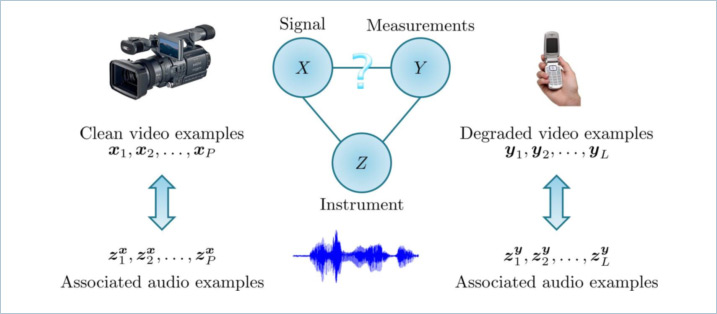
The training sets in this situation can be used to learn
the densities fXZ(x,y) and fYZ(y,z)
but are generally insufficient for determining fY|X(y|x).
The difference between the MSE of an estimator and the lowest possible MSE that could be achieved if fY|X(y|x) was known, is called regret. The regret attained by any estimation strategy depends on the unknown likelihood fY|X(y|x). Our approach in this work is to design an estimator whose regret for the worst-case likelihood, which is consistent with our knowledge of fXY(x,y) and fYZ(y,z), is minimal. We call this technique the partial knowledge minimax regret estimator.
Reference
Software Download
Usage:
A simple example of its use on synthetic data can be found in TestMinimax.m. In this example, X, Y and Z are jointly Gaussian random vectors. The minimax regret estimator is supplied with two unpaired sets of paired realizations { xn, zn} and { yn, zn}. Its MSE is compared with that of the MMSE estimator, which knows the true joint distribution of X and Y.
|
|

