 |
Software & Hardware
Software
The Modulated Wideband Converter: Sub-Nyquist Sampling of Sparse Wideband Analog Signals
Moshe Mishali and Yonina C. EldarWebpage and simulations written by Moshe Mishali and Yilun Chen.
Introduction
Conventional sub-Nyquist sampling methods for analog signals exploit prior information about the spectral support. A more challenging problem is spectrum-blind sub-Nyquist sampling of multiband signals. For example, cognitive radio receivers face with this kind of problem whenever sensing the RF spectrum at their surroundings. The modulated wideband converter (MWC) is the first system for sub-Nyquist sampling, which can be realized with existing devices and handle wideband analog signals. This enables, for example, realizing a carrier-unaware cognitive radio receiver, as further described in this paper. This page describes the MWC system and provides two simulation packages for signal recovery from samples obtained by the MWC (see below on the differences between these packages). The recovery performance is measured in Monte-Carlo setup, namely by using the MWC for sampling and reconstruction a large number of randomly-drawn multiband inputs, and reporting the average recovery accuracy over these test inputs. These packages were used to create the figures in the research papers. A simplified version of these simulations, which is described in this page, simulates a single realization of a multiband input via a convenient graphical user interface (GUI). In addition to signal reconstruction, this page demonstrates carrier frequencies estimation and information bits decoding of concurrent narrowband digital transmissions.
Signal model. The Fourier transform of wideband signals often occupies only a small portion of a wide spectrum, with unknown frequency support. For example: in wideband communication, the receiver sees the sum of several radio-frequency transmissions. Each signal is modulated around an unknown and different carrier frequency.

The system. With an efficient hardware implementation and low computational load on the supporting digital processing, the modulated wideband converter (MWC) can blindly sample multiband analog signals at a low sub-Nyquist rate. The MWC first multiplies the analog signal by a bank of periodic waveforms. Then the product is lowpass filtered and sampled uniformly at a low rate. The waveform period and the uniform rate can be made as low as the expected width of each band, which is orders of magnitude smaller than the Nyquist rate. Reconstruction relies on recent ideas developed in the context of analog compressed sensing, and is comprised of a digital step which recovers the spectral support. The MWC enables baseband processing, namely generating a low rate sequence corresponding to any information band of interest from the given samples, without going through the high Nyquist rate. In the broader context of Nyquist sampling, the MWC scheme has the potential to break through the bandwidth barrier of state-of-the-art analog conversion technologies such as interleaved converters.


Reference
- M. Mishali and Y. C. Eldar, "From Theory to Practice: Sub-Nyquist Sampling of Sparse Wideband Analog Signals", IEEE Journal of Selected Topics on Signal Processing, vol. 4, no. 2, pp. 375-391, April 2010.
- M. Mishali, Y. C. Eldar, O. Dounaevsky and E. Shoshan, "Xampling: Analog to Digital at Sub-Nyquist Rates", IET Circuits, Devices & Systems, vol. 5, no. 1, pp. 8–20, Jan. 2011.
- M. Mishali and Y. C. Eldar, "Blind Multi-Band Signal Reconstruction: Compressed Sensing for Analog Signals", IEEE Trans. on Signal Processing, vol. 57, no. 3, pp. 993-1009, March 2009.
- M. Mishali and Y. C. Eldar, "Reduce and Boost: Recovering Arbitrary Sets of Jointly Sparse Vectors", IEEE Trans. on Signal Processing, vol. 56, no. 10, pp. 4692-4702, October 2008.
- M. Mishali and Y. C. Eldar, "Expected RIP: Conditioning of The Modulated Wideband Converter", Information theory workshop (ITW), pp. 343-347, October 2009.
Software Download
- Matlab package that simulates sampling by the analog system. The MWC consists of an RF front-end whose intermediate nodes are non-bandlimited signals. In this setting, computing the samples that would have been obtained by the hardware becomes a tricky task. This package sets the MWC parameters properly and also uses a dense time-grid in order to ensure sufficient approximation in computing the analog samples.
The simulations in this paper were generated by this package.
Usage:
1. Download from here and unzip.
2. Use start.m to run the simulations (can last many hours).
3. Use GenFigs.m to generate the figures from the saved results.
- A simulation package of the MWC of a digital counterpart of the RF front-end. In this setting, the input signal is a vector of samples which is assumed to have a multiband support in the DFT domain (which in general is not true for a set of samples of an analog multiband input). Although this demonstration is not simulating the analog system, it has a prominent advantage -- the runtime is considerable shorter, since there is no need to approximate the input on a dense time grid. It can help to ease the understanding of the system and the simulation setup, which is similar to the previous package, up to a few different line codes (see the comments in the body of the CTF block below).
Usage:
1. download from here, unzip and run demo.m.

Detailed guidelines for the software usage:
Overview
The modulated wideband converter (MWC) is comprised of two stages: sampling and reconstruction.
In the sampling stage, the input signal enters a bank of multiple channels simultaneously. In each channel, the input signal is multiplied by a mixing function. The mixing function is designed to be a periodic random bit-sequence. Its purpose is to spread the spectrum such that a portion of energy from each band appears in the baseband. After mixing, the signal spectrum is first truncated by a lowpass filter and then sampled at a low rate corresponding to the lowpass cutoff, yielding multiple channels of low-rate digital samples.
In the reconstruction stage, the low-rate digital samples enter the continuous-to-finite (CTF) block for spectrum support estimation. Once the unknown support of the spectrum is determined, the active bands of the input signal are reconstructed by digital processing and mature DAC technology.
Signal Model
The signal of interest is a multiband signal consisting 3 pairs of bands (total N = 6 bands, as depicted in Fig. 1). Each band is of width B = 50MHz and of energy 1, 2, and 3. Ttime offsets are specifed by Taui, to better visualize the results. The Nyquist rate of the multiband signal is supposed to be as high as 10GHz.
SNR = 10;
N = 6;
B = 50e6;
fnyq = 10e9;
Ei = [1 2 3];
Tnyq = 1/fnyq;
R = 1;
K = 91;
K0 = 10;
L = 195;
TimeResolution = Tnyq/R;
TimeWin = [0 L*R*K-1 L*R*(K+K0)-1]*TimeResolution;
Taui = [0.7 0.4 0.3]*max(TimeWin);
fprintf(1,'---------------------------------------------------------------------------------------------\n');
fprintf(1,'Signal model\n');
fprintf(1,' N= %d, B=%3.2f MHz, fnyq = %3.2f GHz\n', N, B/1e6, fnyq/1e9);
Sampling Parameters
We use 50 low-rate sampling channels to sample the 10GHz multiband signal. The sampling rate for each channel is fs = 10GHz/195 = 51.3MHz. Therefore, the actual sampling rate is 51.3MHz*50 = 2.56GHz.
ChannelNum = 50;
L = 195;
M = 195;
fp = fnyq/L;
fs = fp;
m = ChannelNum;
SignPatterns = randsrc(m,M);
Tp = 1/fp;
Ts = 1/fs;
L0 = floor(M/2);
L = 2*L0+1;
fprintf(1,'---------------------------------------------------------------------------------------------\n');
fprintf(1,'Sampling parameters\n');
fprintf(1,' fp = %3.2f MHz, m=%d, M=%d\n',fp/1e6,m,M);
fprintf(1,' L0 = %d, L=%d, Tp=%3.2f uSec, Ts=%3.2f uSec\n', L0, L, Tp/1e-6, Ts/1e-6);
Signal Representation
Now we generate the input signal using the following codes. The carriers of the signal are randomly assigned.
t_axis = TimeWin(1) : TimeResolution : TimeWin(end);
t_axis_sig = TimeWin(1) : TimeResolution : TimeWin(2);
fprintf(1,'---------------------------------------------------------------------------------------------\n');
fprintf(1,'Continuous representation\n');
fprintf(1,' Time window = [%3.2f , %3.2f) uSec\n',TimeWin(1)/1e-6, TimeWin(2)/1e-6 );
fprintf(1,' Time resolution = %3.2f nSec, grid length = %d\n', TimeResolution/1e-9, length(t_axis));
fprintf(1,'---------------------------------------------------------------------------------------------\n');
fprintf(1,'Generating signal\n');
x = zeros(size(t_axis_sig));
fi = rand(1,N/2)*(fnyq/2-2*B) + B;
for n=1:(N/2)
x = x+sqrt(Ei(n)) * sqrt(B)*sinc(B*(t_axis_sig-Taui(n))) .* cos(2*pi*fi(n)*(t_axis_sig-Taui(n)));
end
han_win = hann(length(x))';
x = x.*han_win;
x = [x, zeros(1,R*K0*L)];
Sorig = [];
Starts = ceil((fi-B/2)/fp-0.5+L0+1);
Ends = ceil((fi+B/2)/fp-0.5+L0+1);
for i=1:(N/2)
Sorig = union (Sorig, Starts(i):Ends(i));
end
Sorig = union(Sorig, L+1-Sorig);
Sorig = sort(Sorig);
---------------------------------------------------------------------------------------------
Continuous representation
Time window = [0.00 , 1.77) uSec
Time resolution = 0.10 nSec, grid length = 19695
---------------------------------------------------------------------------------------------
Generating signal
We run the following commands in MATLAB to see the spectrum of the signal.
>> figure, plot(linspace(-5,5,length(x)),abs(fftshift(fft(x)))),grid on
>> title('Spectrum of x'), xlabel('Frequency (GHz)'), ylabel('Magnitude')
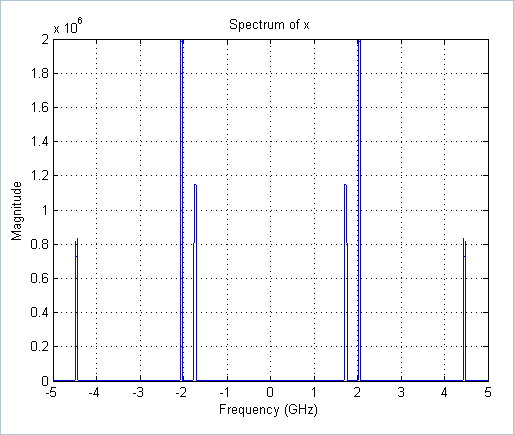
The indices of active bands are:
>> Sorig
Sorig=
11 12 58 59 64 65 131 132 137 138 184 185
Noise Generation
The white Gaussian noise is genereated such that its spectrum is in [-fnyq/2, fnyq/2].
noise_nyq = randn(1,(K+K0)*L);
noise = interpft(noise_nyq, R*(K+K0)*L);
NoiseEnergy = norm(noise)^2;
SignalEnergy = norm(x)^2;
CurrentSNR = SignalEnergy/NoiseEnergy;
Mixing
Now we mix the input signal and noise with random periodical functions.
fprintf(1,'Mixing\n');
MixedSigSequences = zeros(m,length(t_axis));
for channel=1:m
MixedSigSequences(channel,:) = MixSignal(x,t_axis,SignPatterns(channel,:),Tp);
end
MixedNoiseSequences = zeros(m,length(t_axis));
for channel=1:m
MixedNoiseSequences(channel,:) = MixSignal(noise,t_axis,SignPatterns(channel,:),Tp);
end
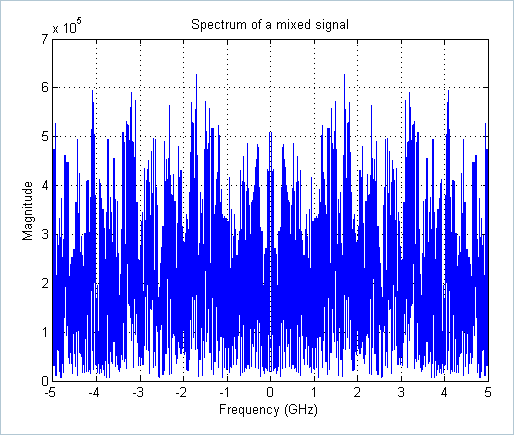
The random mixing function aliases energies from each bands into the baseband. This is the key step that enables the following baseband operation without losing information.
>> figure,plot(linspace(-5,5,length(x)),abs(fftshift(fft(MixedSigSequences(1,:))))), grid on
>> title('Spectrum of a mixed signal'), xlabel('Frequency (GHz)'), ylabel('Magnitude')
Analog Low-pass Filtering and Actual Sampling
For each channel, we filter the mixed channel with an ideal low pass filter. Then we downsample the high-rate input sequences (19695 samples for each channel) into low-rate ones (101 samples for each channel).
fprintf(1,'Filtering and decimation (=sampling)\n');
temp = zeros(1,K+K0);
temp(1) = 1;
lpf_z = interpft(temp,length(t_axis))/R/L;
SignalSampleSequences = zeros(m,K+K0);
NoiseSampleSequences = zeros(m,K+K0);
fprintf(1,' Channel ');
decfactor = L*R;
for channel = 1:m
fprintf(1,'.'); if ( (mod(channel,5)==0) || (channel==m)) fprintf(1,'%d',channel); end
SignalSequence = MixedSigSequences(channel,:);
NoiseSequence = MixedNoiseSequences(channel,:);
DigitalSignalSamples(channel, :) = FilterDecimate(SignalSequence,decfactor,lpf_z);
DigitalNoiseSamples(channel, :) = FilterDecimate(NoiseSequence,decfactor,lpf_z);
end
Digital_time_axis = downsample(t_axis,decfactor);
DigitalLength = length(Digital_time_axis);
fprintf(1,'\n---------------------------------------------------------------------------------------------\n');
fprintf(1,'Sampling summary\n');
fprintf(1,' %d channels, each gives %d samples\n',m,DigitalLength);
Filtering and decimation (=sampling)
Channel .....5.....10.....15.....20.....25.....30.....35.....40.....45.....50
---------------------------------------------------------------------------------------------
Sampling summary
50 channels, each gives 101 samples
CTF Block
Next, we use CTF block to recover the support of active bands. The following results indicate that we successfully recover the support.
fprintf(1,'---------------------------------------------------------------------------------------------\n');
fprintf(1,'Entering CTF block\n');
S = SignPatterns;
theta = exp(-j*2*pi/L);
F = theta.^([0:L-1]'*[-L0:L0]);
np = 1:L0;
nn = (-L0):1:-1;
dn = [ (1-theta.^nn)./(1-theta.^(nn/R))/(L*R) 1/L (1-theta.^np)./(1-theta.^(np/R))/(L*R)];
D = diag(dn);
A = S*F*D;
A = conj(A);
SNR_val = 10^(SNR/10);
DigitalSamples = DigitalSignalSamples + DigitalNoiseSamples*sqrt(CurrentSNR/SNR_val);
Q = DigitalSamples* DigitalSamples';
NumDomEigVals= FindNonZeroValues(eig(Q),5e-8);
[V,d] = eig_r(Q,min(NumDomEigVals,2*N));
v = V*diag(sqrt(d));
[u, RecSupp] = RunOMP_Unnormalized(v, A, N, 0, 0.01, true);
RecSuppSorted = sort(unique(RecSupp));
if (is_contained(Sorig,RecSuppSorted) && (rank(A(:,RecSuppSorted)) == length(RecSuppSorted)))
Success= 1;
fprintf('Successful support recovery\n');
else
Success = 0;
fprintf('Failed support recovery\n');
end
---------------------------------------------------------------------------------------------
Entering CTF block
Successful support recovery
Recover the Signal
Once we determine the support, we can easily reconstruct each signal band by a direct pseudoinverse operation. The signal bands are then modulated to their corresponding carrier frequencies.
All the band signals are then modulated to their corresponding carrier frequencies.
A_S = A(:,RecSuppSorted);
hat_zn = pinv(A_S)*DigitalSamples;
hat_zt = zeros(size(hat_zn,1),length(x));
for ii = 1:size(hat_zt,1)
hat_zt(ii,:) = interpft(hat_zn(ii,:),L*R*length(hat_zn(ii,:)));
end
x_rec = zeros(1,length(x));
for ii = 1:size(hat_zt,1)
x_rec = x_rec+hat_zt(ii,:).*exp(j*2*pi*(RecSuppSorted(ii)-L0-1)*fp.*t_axis);
end
x_rec = real(x_rec);
sig = x + noise*sqrt(CurrentSNR/SNR_val);
Analysis & Plots
We finally plot all the results here.
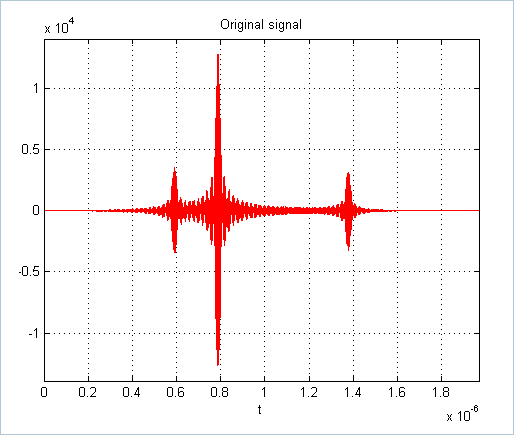
figure,
plot(t_axis,x,'r'), axis([t_axis(1) t_axis(end) 1.1*min(x) 1.1*max(x) ])
title('Original signal'), xlabel('t')
grid on
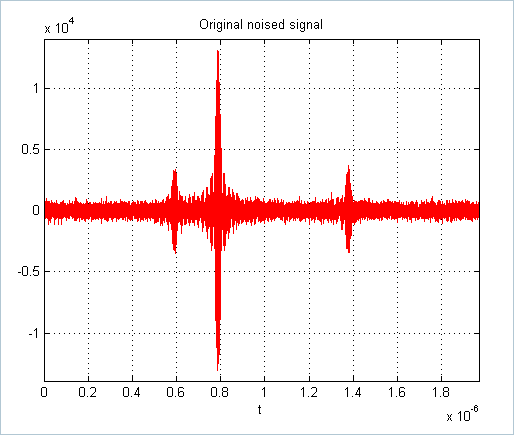
figure,plot(t_axis,sig,'r'), axis([t_axis(1) t_axis(end) 1.1*min(x) 1.1*max(x) ])
title('Original noised signal'), xlabel('t')
grid on
figure, plot(t_axis,x_rec), axis([t_axis(1) t_axis(end) 1.1*min(x) 1.1*max(x) ]),
grid on,
title('Reconstructed signal'), xlabel('t')
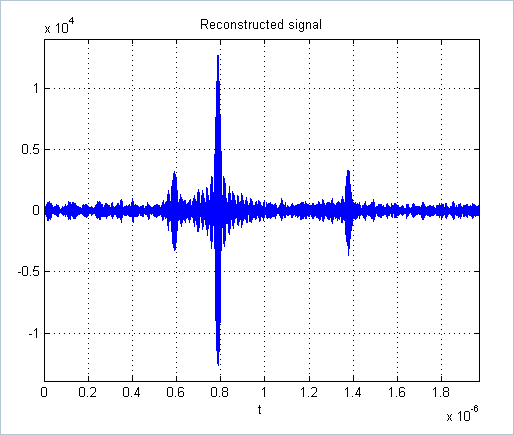
The output SNR is
>> 20*log10(norm(x)/norm(x-x_rec))
ans =
14.9204
Therefore, compared to the conventional Nyquist sampling , the SNR gain is 14.9204 - 10 = 4.9204 (dB).
Note that the simulation above is for a noisy input signal. If the signal is noiseless (this can be implemented by assigning a sufficiently large value to the parameter SNR), then by re-doing the simulation, the pure reconstruction error is calculated to be about 1e-6, which is almost perfect reconstruction.
|
|

