 |
Software & Hardware
Software
Non-Convex Phase Retrieval from STFT Measurements
T. Bendory and Y. C. Eldar
Introduction
The problem of recovering a signal from its Fourier transform magnitude, called phase retrieval, arises in many
areas in engineering and science, such as optics, X-ray crystallography, speech recognition, blind channel estimation
and astronomy. Phase retrieval for one-dimensional signals is an ill-posed problem in most cases. We consider the
closely-related problem of recovering a signal from its phaseless short-time Fourier transform (STFT) measurements.
This problem arises naturally in several applications, such as ultra-short pulse measurements and ptychography.
In contrast to previous works in the field of phase retrieval, we aim at developing a phase retrieval algorithm
that reflects a practical setup, is computationally efficient and enjoys theoretical guarantees.
Main Idea
The algorithm begins by taking the one-dimensional DFT of the acquired information with respect to the frequency
variable (the second variable of the STFT). This transformation reveals the underlying structure of the data and
greatly simplifies the analysis. Then, we suggest recovering the signal by minimizing a non-convex loss function
(frequently called empirical risk or non-linear least-squares) using a gradient algorithm. We propose to initialize
the gradient algorithm by the principle eigenvector (with proper normalization) of an approximation matrix that
approximates the correlation matrix of the underlying signal. This approximation matrix is constructed as the
solution of a simple least-squares problem. For a detailed description and analysis of the algorithm,
see "Non-Convex Phase Retrieval from STFT Measurements"
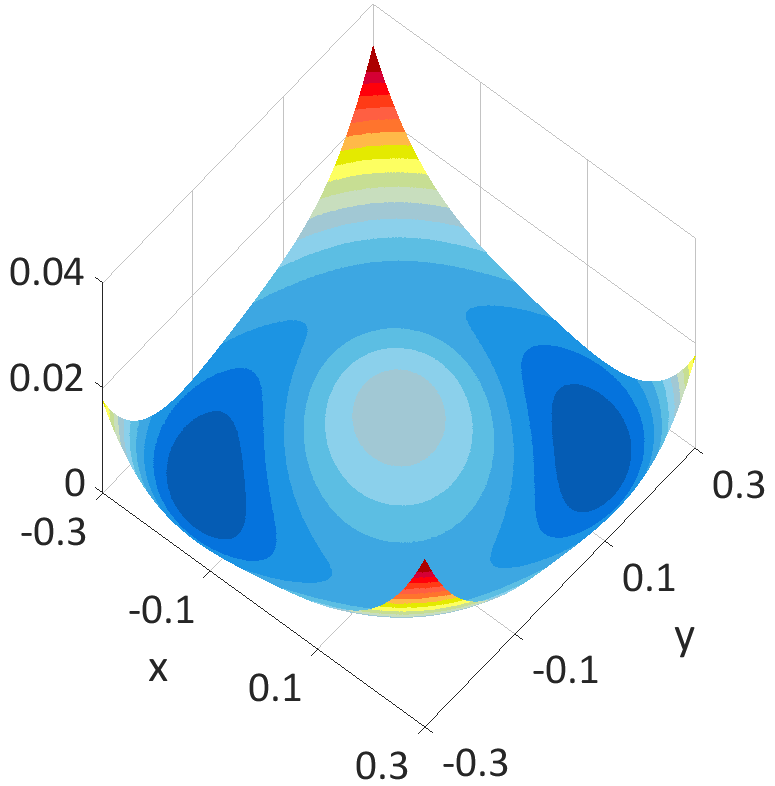
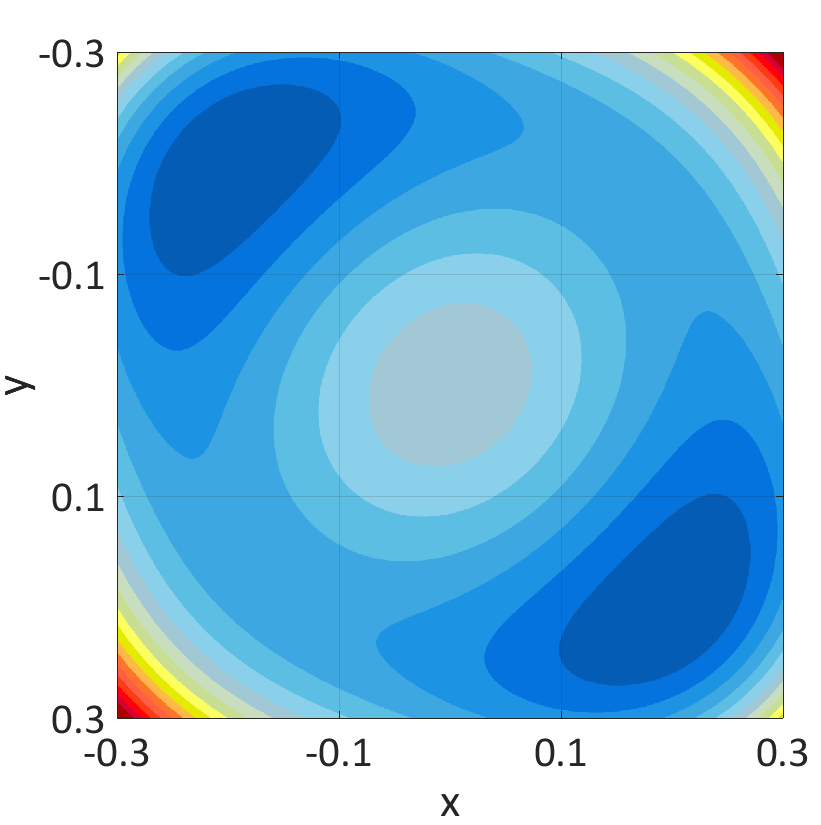
side view
view from above
The figure presents the two-dimensional plane (first two variables) of the
non-convex
loss function to be minimized of the signal x=[0.2,0.2,0,0,0].
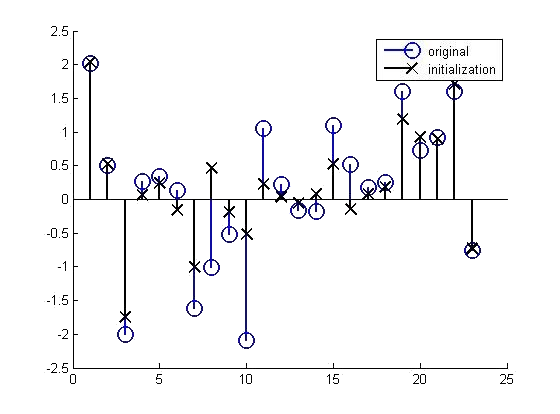
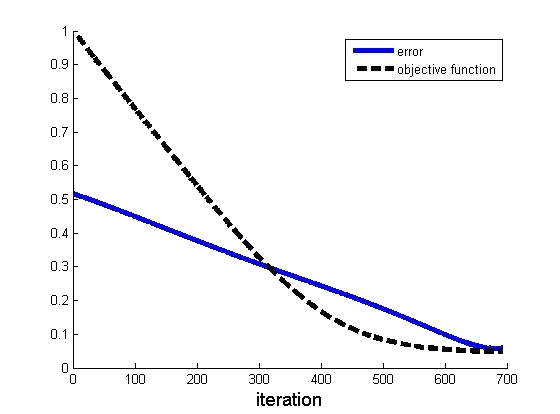
A Representative Example
The following figures show a representative example of the algorithm's performance. The experiment was
conducted on a signal of length N = 23 with L=1, a rectangular window of length W=7 in a noisy environment
of SNR= 20 db. The upper-left and upper-right figures present the initialization and recovered signal versus
the underlying signal, respectively. The figure below presents the error and objective function curves
as a function of the iterations.

References
Software Download
Installation:
1. Unzip.
2. Follow the instructions in the Readme.txt
|
|

