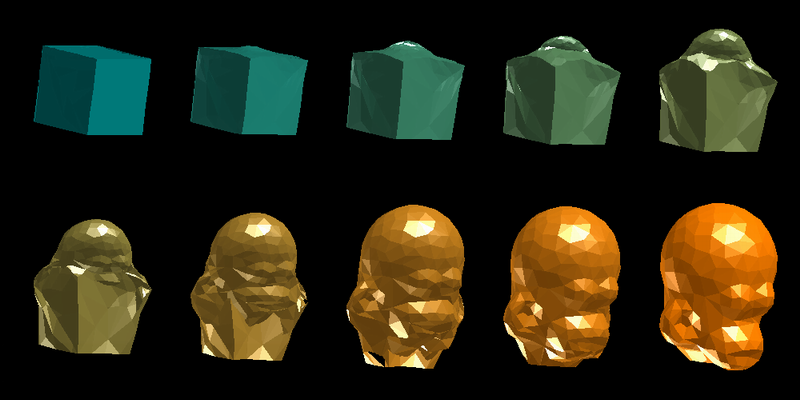by Golubitsky Dany
and Dobrovinsky Ron
Supervised by Sagi Katz
Abstract
Three-Dimensional
(3D) Metamorphosis is
the gradual transformation of a source 3D object through intermediate
objects into a target object. 3D Metamorphosis of polyhedral surfaces
has been a lively topic of research for many years. In order to
generate a pleasing morph sequence, it is usually required to find a
good correspondence between two surfaces before applying an
interpolation. A common approach for finding a correspondence between
two given polyhedra is to look for a common embedding of their
topologies (i.e., their one-skeleton graphs). This is done by
projecting the models onto a common parameterization domain, merging
their one-skeleton graphs in this domain, and projecting the merged
topology back to the original models. In our project, we implement an
algorithm for establishing a correspondence between two disk-like
objects. In order to do it we project both of the object onto
Two-dimensional (2D) ideal disk, merge the two projections to get
topology that can be applied to both of the objects and then project
the merged topology to both of the objects. Thus we get two different
objects with the same amount of vertices, triangles and with the same
correspondence graph. Simple linear interpolation than may be used to
convert one object to another and vice versa.
Process
Overall
In
order to implement
the metamorphosis we have to devide problem into two sub-problems. The
first sub-problem is the establishment of a correspondence from
features on the source object to features on the target object. Once
the correspondence has been established, the second sub-problem is the
creation of a sequence of in-between objects done by interpolating
features of the source object to their corresponding features on the
target object. This step is referred to as the interpolation problem.
In our project we used simple linear interpolation between
corresponding features, focusing on the correspondence problem.
Given two polyhedral surfaces, there are infinitely many ways to
transform an object into another. However, to achieve good-looking
results morphing sequence should seem smooth and continuous maintaining
the shapes of the objects as much as possible during the
transformation. This criterion is subjective and depends on the context
in which the morphing is performed. Another, less subjective criterion
is the prevention of self-intersection throughout the morph.
Various techniques related to the polyhedral surface morphing have been
proposed. A large family of algorithms is based on the construction of
a common mesh which merges the topologies of the given objects
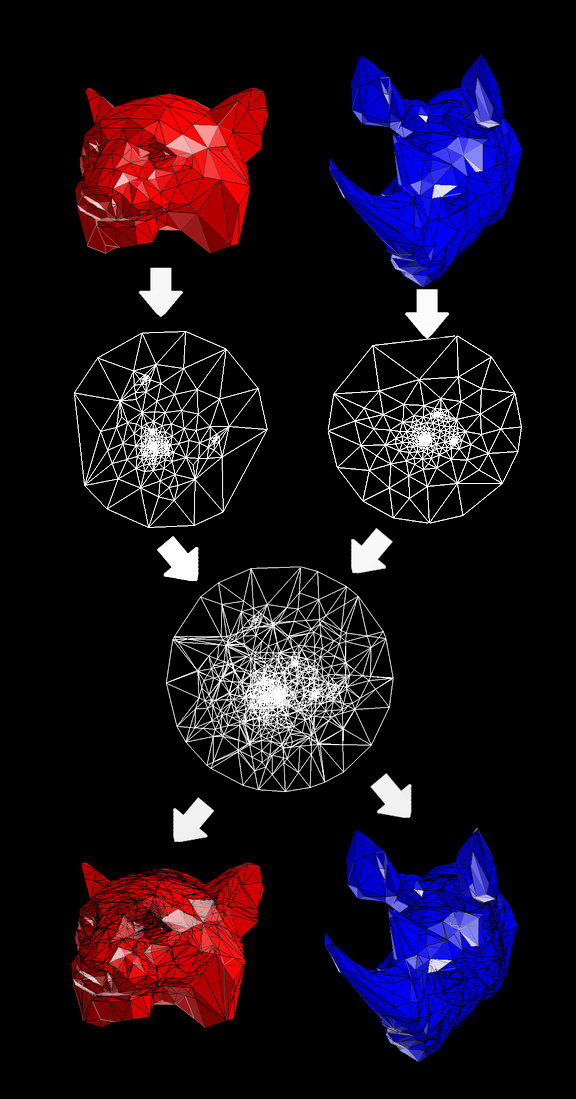
In our project we follow 3 main stages. First, we take two disk-like
objects and create a parametric tiling of them on ideal disks. Second,
we create a metamesh of the objects that can be restored both to object
A and to object B. The restored objects, therefore, will have exactly
the same number of vertices and faces and the same correspondence
between them. Each vertex and each face will have it's place on each
object.
Process overall diagram
Embedding disk-like objects
The
main concern in
embedding disk-like objects is how to map the patches such that the
local geometry of the mesh is preserved as much as possible. There are
couple of methods available. The first (simple) one is barycentric
method. It is relatevely easy to implement but its results are far from
perfect. The second method is harmonic mapping. It produces better
results, but, as we discovered in our project, has a very big
limitation - it can not be aplied to meshes that have triangles with
obtuse angles. You can read about both of this methods in our
Project Report. Here we want to show you two
examples:
Barycenric
mapping example
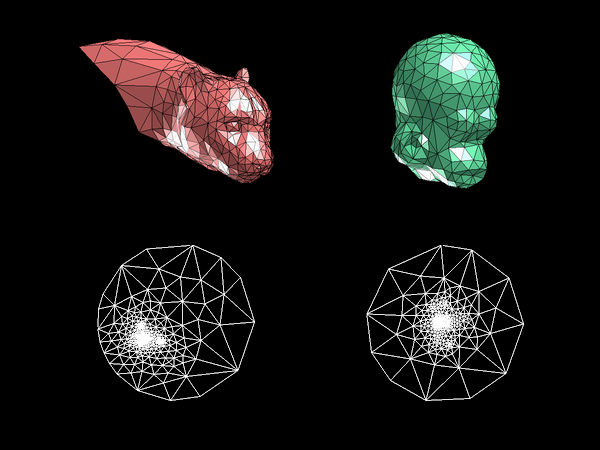
Harmonic
vs. Barycentric mapping of the Cube
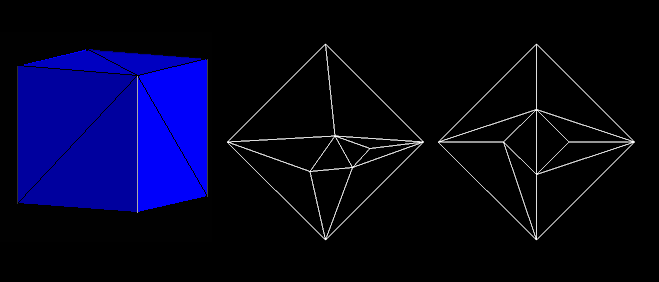
We can see that harmonic mapping (from the
right) gives much better results than barycentric (in the middle).
In order to produce a
full correspondence between two disk-like patches, a common
vertex/edge/face connectivity graph should be built. This is done by
merging the embeddings of the patches. The merge process consists of
three steps: building vertex connectivity matrix and edges matrix,
finding intersection points between the edges, and finally, creating
triangles metamesh containing all the vertices from object A and all
the vertices from object B. All steps are described in our Project Report.
Tools
- The project was
implemented using Matlab program.
- The Video files
processing was made by Virtual Dub application.
Results
Here you can see some examples of
metamorphosises we produced:
Metamorphosis
of a Cube into a
Rhino's
Head [Video
Clip]
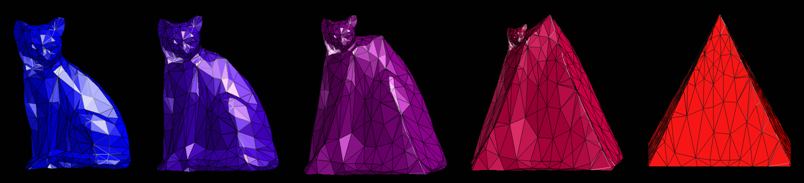
Metamorphosis
of a Cube into a
Rhino's
Head [Video
Clip]
Acknowledgment
We would like to thank our project
supervisor Sagi Katz and Head of the
CGM Laboratory Dr.
Ayellet Tal for their substantial assistance, their
knowledge and cooperation.We also wish to thank all CGM Laboratory
staff and especially Lab Engineer Doron Tal for providing excellent
working conditions and a good atmosphere.
Related Documentation