Yoav Y. Schechner: Research

Optimized Poisson Compressed Sensing Matrix

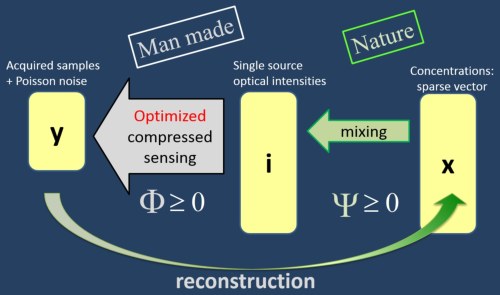
For compressed sensing of Poissonian measurements, there is a need for nonnegative measurement matrices. We seek an optimal measurement matrix that conserves energy. Moreover, the signals pass a known but uncontrolled mixing matrix, before being multiplexed and measured. This situation is relevant to various optical applications. We optimize the measurement matrix by mutual coherence minimization, under nonnegativity and energy conservation constraints. Nonnegativity excludes the known approach of seeking an equiangular tight frame as the optimal matrix. We thus seek a quasi-equiangular frame, which is approximated by a tight frame. Simulation results demonstrate superior reconstruction using our optimized matrices, compared to random nonnegative matrices.

Publications

1. M. Mordechay and Yoav Y. Schechner, “Matrix Optimization for Poisson Compressed Sensing,” Proc. IEEE GlobalSIP, Advances in Signal Processing for Mixed-Signal and Optical Sensing: Hardware to Algorithms pp. 684-688 (2014).

Presentations

1. "Measurement Matrix Optimization for Poisson Compressed Sensing (3 Mb, Powerpoint).

Software

Matlab codes that run the algorithms as described in our paper. Available for non-commercial use. You can use it if you clearly acknowledge the source by citing "Matrix optimization for Poisson compressed sensing" detailed above, in your work.

1. Documented matlab software, (8K ZIP).

Related Research

1. Multiplexed Fluorescence Unmixing
2. Multiplexed Illumination