 |
Software & Hardware
Software
GESPAR: Efficient Phase Retrieval of Sparse Signals
Yoav Shechtman, Amir Beck and Yonina C. Eldar
Introduction
Recovery of a signal from the magnitude of its Fourier transform, also known as phase retrieval, is of great interest in applications such as optical imaging, crystallography and more. Due to the loss of Fourier phase information, the problem (in 1D) is generally ill-posed. A common approach to overcome this ill-posedeness is to exploit prior information on the signal. We develop a method that exploits signal sparsity.
The problem of phase retrieval of a sparse discrete signal can be presented as a set of quadratic equations of the form: yi=xTAix, where x is the unknown sparse vector to be recovered,yi are the measurements, and Ai are the known matrices Ai=FiTFi , where Fi is the i'th row of the discrete Fourier transform (DFT) matrix.
 Coherent-Diffractive-Imaging (CDI) setting, an example where the phase retrieval problem arises: A 2D object is illuminated by a coherent laser beam, and the far-field diffraction intensity pattern is measured. The problem is to recover the object from its far-field diffraction intensity measurement - which corresponds to the magnitude of the object's 2D Fourier transform.
Coherent-Diffractive-Imaging (CDI) setting, an example where the phase retrieval problem arises: A 2D object is illuminated by a coherent laser beam, and the far-field diffraction intensity pattern is measured. The problem is to recover the object from its far-field diffraction intensity measurement - which corresponds to the magnitude of the object's 2D Fourier transform.
We propose GESPAR (GrEedy Sparse PhAse Retrieval): An efficient method for phase retrieval which also leads to good recovery performance. Our algorithm is based on a fast 2-opt local search method applied to a sparsity constrained non-linear optimization formulation of the problem. In essence, GESPAR is a local-search method, where the support of the sought signal is updated iteratively, according to certain selection rules. A local minimum of the objective function is then found given the current support using the damped Gauss Newton algorithm. We demonstrate through numerical simulations that the proposed algorithm is both efficient and more accurate than current techniques.
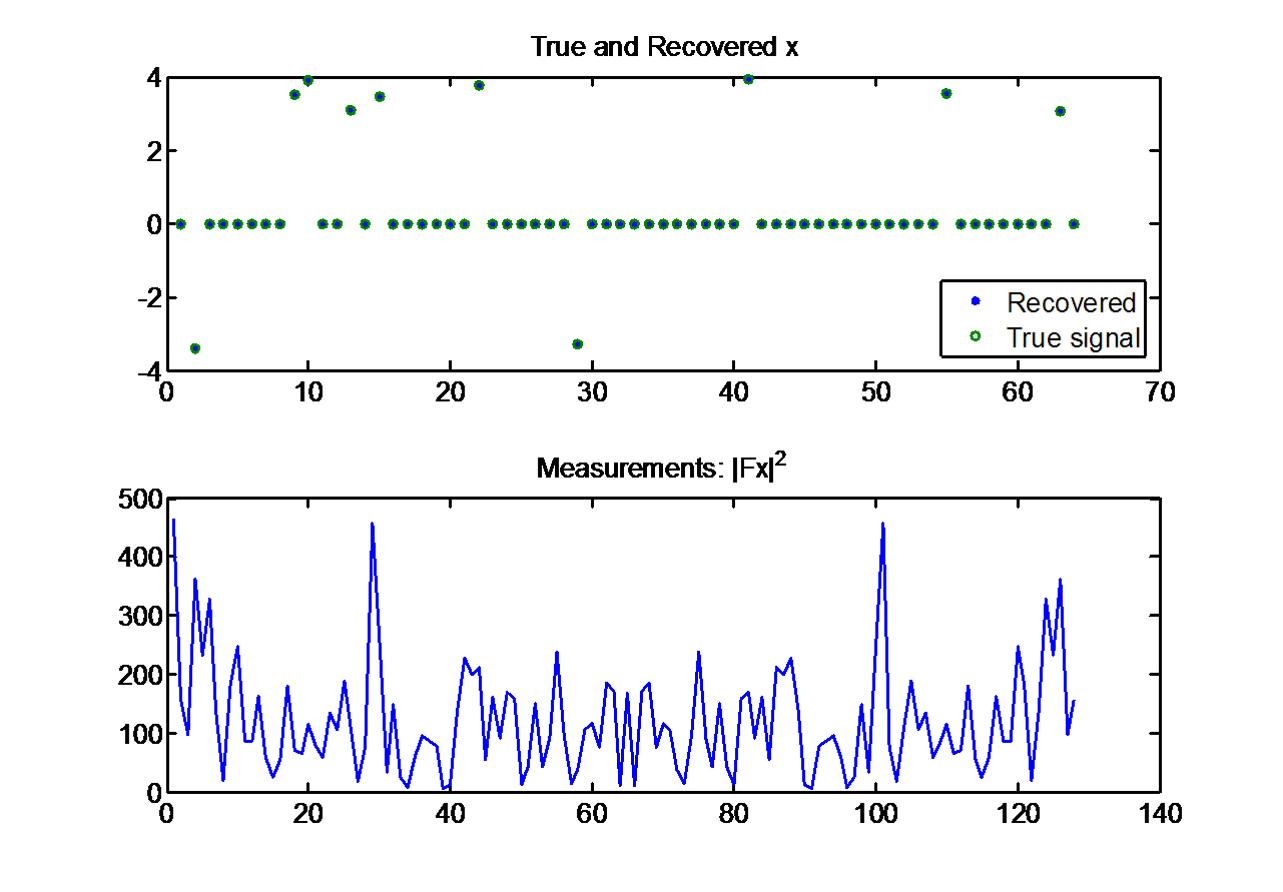
Reconstruction example: A 10 sparse signal x of length 64 is successfully recovered from 128 measurements of its Fourier magnitude.
See the paper for more details.
Reference
Software Download
Installation:
Unzip Gespar - 1D Fourier.zip
Usage:
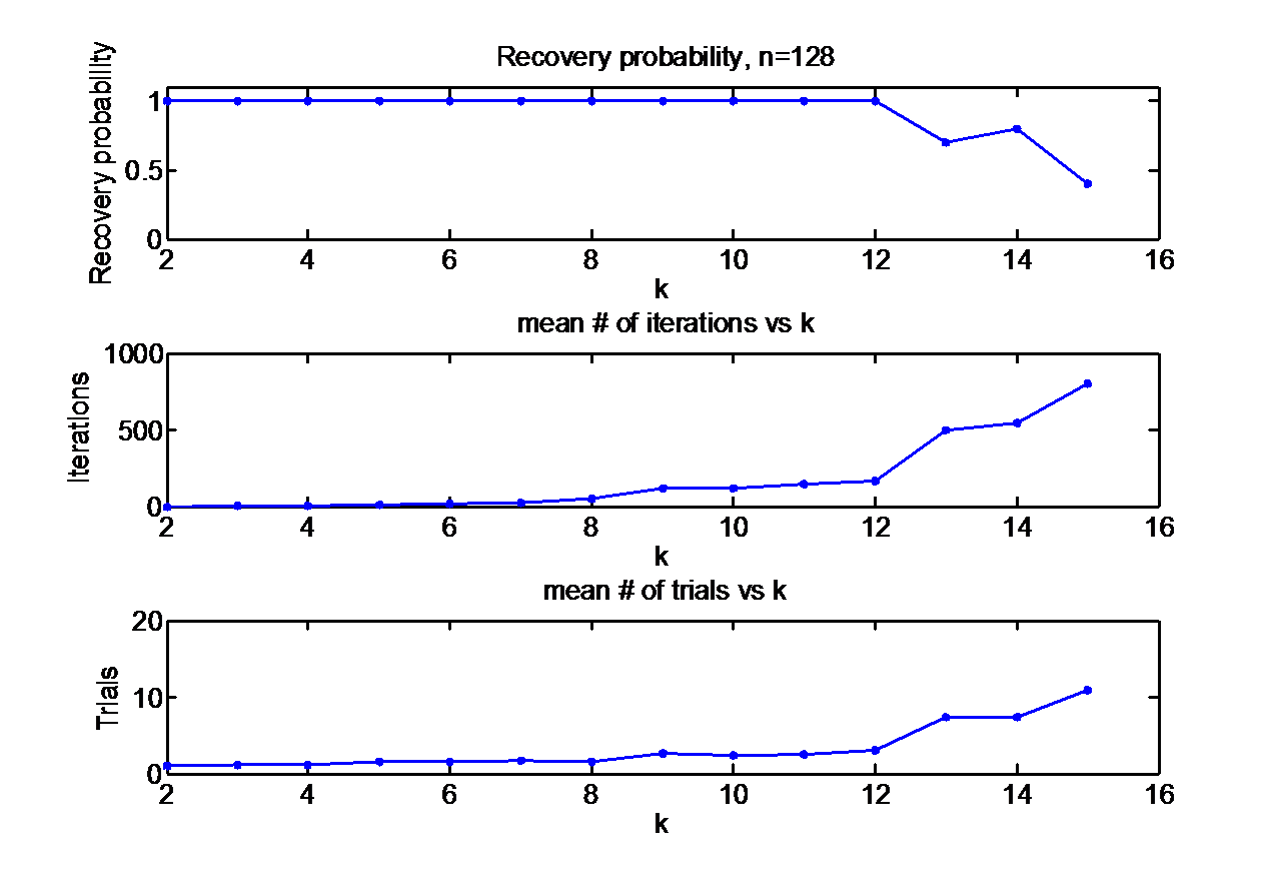
GESPAR_sim.m is a script that runs the following sparse recovery simulation:
For each sparsity value k from the vector kVec:
- Randomly create a k sparse signal x of length n/2.
- Recover x from n measurements of its Fourier transform magnitude.
- Repeat maxIt times for each sparsity level.
The results are summarized in a plot similar to the one below (depending on implementation parameters):
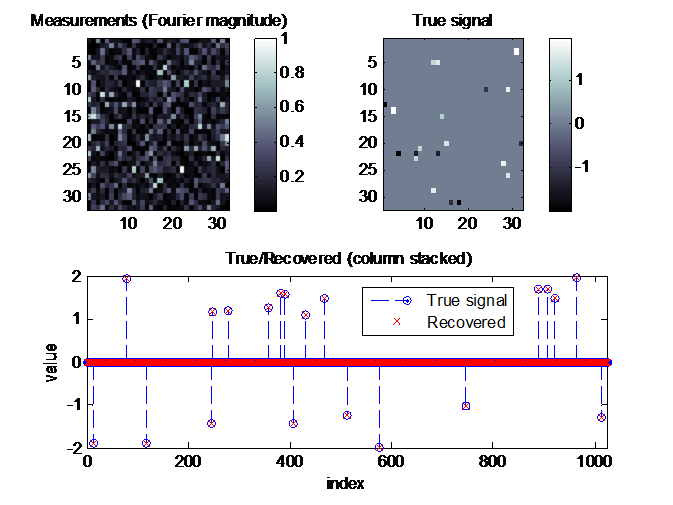
GESPAR_sim2D.m is a script that runs a 2D Fourier phase-retrieval example, on a k sparse 2D image. The result is shown in a figure similar to the one below (depending on implementation parameters):
|
|

